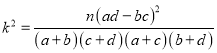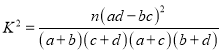题目内容
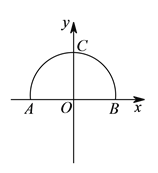
【题目】在△ABC中,已知内角 ![]() ,边
,边 ![]() .设内角B=x,△ABC的面积为y.
.设内角B=x,△ABC的面积为y.
(1)求函数y=f(x)的解析式和定义域;
(2)当角B为何值时,△ABC的面积最大.
【答案】
(1)解:∵ ![]() ,且A+B+C=π
,且A+B+C=π
∴ ![]() 即
即 ![]()
由正弦定理可得, ![]()
∴AC= ![]() =4sinx
=4sinx
y= ![]() sinA=4
sinA=4 ![]() sinxsin(
sinxsin( ![]() )
) ![]()
(2)解:y=4 ![]() sinxsin(
sinxsin( ![]() )=
)= ![]()
= ![]()
=3sin2x+2 ![]() ×
× ![]()
= ![]() +
+ ![]() (﹣
(﹣ ![]() )
)
当 ![]() 即x=
即x= ![]() 时,y取得最大值3
时,y取得最大值3 ![]()
∴B= ![]() 时,△ABC的面积最大为3
时,△ABC的面积最大为3 ![]()
【解析】(1)由已知角A及三角形的内角和定理可求x的范围,然后由正弦定理, ![]() 可利用x表示AC,代入三角形的面积公式,即可求解(2)利用两角差的正弦公式及辅助角公式对(1)中的函数关系进行化简,结合正弦函数的性质即可求解取得最大值时的x即B及相应的最大值
可利用x表示AC,代入三角形的面积公式,即可求解(2)利用两角差的正弦公式及辅助角公式对(1)中的函数关系进行化简,结合正弦函数的性质即可求解取得最大值时的x即B及相应的最大值

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】在一次爱心捐款活动中,小李为了了解捐款数额是否和居民自身的经济收入有关,随机调査了某地区的![]() 个捐款居民每月平均的经济收入. 在捐款超过
个捐款居民每月平均的经济收入. 在捐款超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个,达到
个,达到![]() 元的有
元的有![]() 个;在捐款不超过
个;在捐款不超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个.
个.
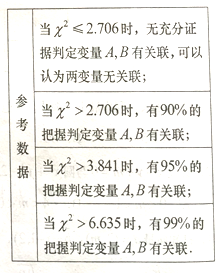
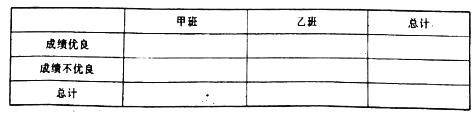
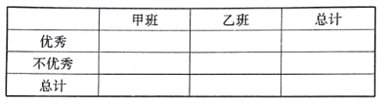
(1)在下图表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否超过
以上的把握认为捐款数额是否超过![]() 元和居民毎月平均的经济收入是否达到
元和居民毎月平均的经济收入是否达到![]() 元有关?
元有关?
(2)将上述调查所得到的频率视为概率. 现在从该地区大量居民中,采用随机抽样方法毎次抽取![]() 个居民,共抽取
个居民,共抽取![]() 次,记被抽取的
次,记被抽取的![]() 个居民中经济收入达到
个居民中经济收入达到![]() 元的人数为
元的人数为![]() ,求
,求![]() 和期望
和期望![]() 的值.
的值.
每月平均经济收入达到 | 每月平均经济收入没有达到 | 合计 | |
捐款超过 | |||
捐款不超过 | |||
合计 |
附: 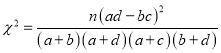 ,其中
,其中![]()