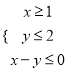题目内容
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)(ⅰ)见解析;(ⅱ)
;(2)(ⅰ)见解析;(ⅱ)![]() .
.
【解析】试题分析:(1)由题意可知, ![]() ,解得
,解得![]() ,可求得半径
,可求得半径![]() ,得圆的方程.
,得圆的方程.
(2)(i)设直线l的方程为![]() ,与圆的方程联立,可得
,与圆的方程联立,可得![]() ,利用韦达定理即可证明;
,利用韦达定理即可证明;
(ii)表示 ![]()
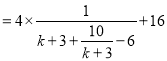 再求最值即可.
再求最值即可.
试题解析:(1)设圆心![]() 的坐标为
的坐标为![]() ,则
,则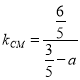 ,又
,又![]() ,
,
由题意可知, ![]() ,则
,则![]() ,
,
故![]() ,所以
,所以![]() ,即半径
,即半径![]() .
.
故圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
由![]() 得:
得: ![]() ,
,
所以![]() ,
, ![]() .
.
(ⅰ)![]() 为定值,
为定值,
(ⅱ)![]()
![]()
![]()
![]()
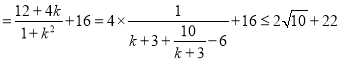
(当且仅当![]() ,即
,即![]() 时等号成立)
时等号成立)
故![]() 的最大值为
的最大值为![]() .
.
点睛:本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.

练习册系列答案
相关题目