题目内容
1.已知数列{an},且an=$\frac{1}{{{n^2}+n}}$,则数列{an}前100项的和等于( )| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{101}{102}$ | D. | $\frac{99}{101}$ |
分析 由已知中an=$\frac{1}{{{n^2}+n}}$=$\frac{1}{n}$$-\frac{1}{n+1}$,利用裂项相消法,可得答案.
解答 解:∵an=$\frac{1}{{{n^2}+n}}$=$\frac{1}{n}$$-\frac{1}{n+1}$,
∴数列{an}前100项的和S=1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{100}-\frac{1}{101}$=$1-\frac{1}{101}$=$\frac{100}{101}$,
故选:A
点评 本题考查的知识点是数列求和,熟练掌握裂项相消法,是解答的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
6.如图,在棱长为3的正方体ABCD-A1B1C1D1中,点C1到平面A1BD的距离为( )
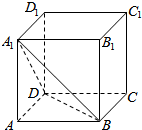

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
11.已知数列{an}中,a2=102,an+1-an=4n,则数列$\left\{{\frac{a_n}{n}}\right\}$的最小项是( )
| A. | 第6项 | B. | 第7项 | C. | 第8项 | D. | 第9项 |