题目内容
【题目】已知数列![]() 满足
满足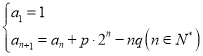 ,其中
,其中![]() .
.
(1)若数列前四项![]() ,
,![]() ,
,![]() ,
,![]() 依次成等差数列,求
依次成等差数列,求![]() ,
,![]() 的值;
的值;
(2)若![]() ,且数列
,且数列![]() 为等比数列,求
为等比数列,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() 是数列
是数列![]() 的最小项,求
的最小项,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)答案不唯一,见解析 (3)
(2)答案不唯一,见解析 (3)![]()
【解析】
(1)由已知求出![]() ,由等差数列的定义得
,由等差数列的定义得![]() 的方程可求解;
的方程可求解;
(2)由![]() 求出
求出![]() 值,代入已知递推式求出
值,代入已知递推式求出![]() ,验证它是等比数列;
,验证它是等比数列;
(3)当![]() 时,用累加法求得
时,用累加法求得![]() ,由
,由![]() 恒成立得,
恒成立得,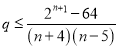 恒成立.用作差法证明数列
恒成立.用作差法证明数列![]() 是递增数列,从而可得最小值,得
是递增数列,从而可得最小值,得![]() 的一个范围,再由
的一个范围,再由![]() 得
得![]() 的另外一些范围后可得
的另外一些范围后可得![]() 的范围
的范围
(1)由已知递推式可得,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() .
.
由等差数列知,![]() ,得
,得![]() ;
;
(2)![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,
,![]() ,满足题意;
,满足题意;
当![]() 时,由累加法得
时,由累加法得![]() ,满足题意;
,满足题意;
(3)![]() 时,
时,
![]() ,
,
![]()
![]() ,
,
当![]() 时,由
时,由![]() 恒成立得,
恒成立得,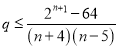 恒成立.
恒成立.
设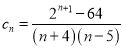 ,只需求出
,只需求出![]() 的最小值.
的最小值.
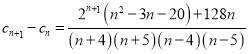 .
.
当![]() 时,
时,![]() ,有
,有![]() ;
;
当![]() 时,直接验证
时,直接验证![]() ;
;
故![]() 为最小值,其值为
为最小值,其值为![]() ,∴
,∴![]() ;
;
当![]() 时,需满足
时,需满足![]() 恒成立,
恒成立,
对![]() 验证,
验证,
![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() .
.
综上,![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目