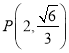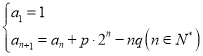题目内容
【题目】已知点![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() ),都在函数
),都在函数![]() (
(![]() ,
,![]() )的图像上;
)的图像上;
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等比数列;
是等比数列;
(2)设![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,若函数
,若函数![]() 与函数
与函数![]() 的图像有公共点
的图像有公共点![]() ,求证:
,求证:![]() 在直线
在直线![]() 上;
上;
(3)设![]() ,
,![]() (
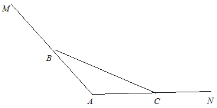
(![]() ),过点
),过点![]() 、
、![]() 的直线
的直线![]() 与两坐标轴围成的三角形面积为
与两坐标轴围成的三角形面积为![]() ,问:数列
,问:数列![]() 是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
【答案】(1)证明见解析;(2)证明见解析;(3)存在,![]() .
.
【解析】
(1)结合指数函数性质,根据等比数列定义进行论证;
(2)先求反函数,再利用反证法证明结论;
(3)先根据点斜式得直线![]() 方程,再根据截距以及三角形面积公式求出
方程,再根据截距以及三角形面积公式求出![]() ,再利用数列单调性确定其最大值.
,再利用数列单调性确定其最大值.
(1)设数列![]() 公差为
公差为![]()
因为![]() 在函数
在函数![]() 上,所以
上,所以![]()
因此数列![]() 是等比数列;
是等比数列;
(2)![]()
假设![]() 不在直线
不在直线![]() 上,所以
上,所以![]()
![]() ,即M不在
,即M不在![]() 上,与
上,与![]() 为函数
为函数![]() 与函数
与函数![]() 的图像有公共点矛盾,所以
的图像有公共点矛盾,所以![]() 在直线
在直线![]() 上;
上;
(3)因为![]() ,
,![]() ,所以
,所以![]()
![]() 、
、![]()
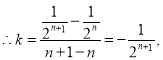
![]()
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,![]()
![]()
所以![]() 为单调递减数列,其最大项为
为单调递减数列,其最大项为![]()

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.