题目内容

【题目】设a∈R，若不等式恒成立，则实数a的取值范围是_____．

【答案】[4﹣6，4+6]

【解析】

由题意可得|x3|+|x3|+8≥（4﹣a）x恒成立，讨论x＞0，x＜0，运用基本不等式，可得最值，进而得到所求范围．

|x3|+|x3|+ax≥4x﹣8恒成立，

即为|x3|+|x3|+8≥（4﹣a）x恒成立，

当x＞0时，可得4﹣a≤|x2|+|x2|的最小值，

由|x2|+|x2||x2x2|2x22x236，

当且仅当x3＝2即x取得最小值6，即有4﹣a≤6，则a≥4﹣6；

当x＜0时，可得4﹣a≥﹣[|x2|+|x2|]的最大值，

由|x2|+|x2|2x22x236，

当且仅当x3＝﹣2即x取得最大值﹣6，即有4﹣a≥﹣6，则a≤4+6，

综上可得4﹣6a≤4+6，

故答案为：[4﹣6，4+6]．

练习册系列答案
相关题目

【题目】新高考取消文理科，实行“”模式，成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况，随机调查50人，并把调查结果制成下表：

年龄（岁）

频数

5

15

10

10

5

5

了解

4

12

6

5

2

1

（1）把年龄在称为中青年，年龄在称为中老年，请根据上表完成列联表，是否有95%的把握判断对新高考的了解与年龄（中青年、中老年）有关？

了解新高考

不了解新高考

总计

中青年

中老年

总计

附：.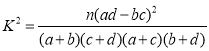

0.050

0.010

0.001

3.841

6.635

10.828

（2）若从年龄在的被调查者中随机选取3人进行调查，记选中的3人中了解新高考的人数为，求的分布列以及.

【题目】已知为等差数列，各项为正的等比数列的前项和为，，，__________.在①；②；③这三个条件中任选其中一个，补充在横线上，并完成下面问题的解答（如果选择多个条件解答，则以选择第一个解答记分）.

（1）求数列和的通项公式；

（2）求数列的前项和.

【题目】已知，其中．

（1）当时，设函数，求函数的极值．

（2）若函数在区间上递增，求的取值范围；

（3）证明：．

【题目】如图，椭圆的左、右焦点分别为、，，点A为椭圆C上异于左右顶点的任意一点，A关于原点O的对称点为B，，且．

（Ⅰ）求椭圆C的标准方程；

（Ⅱ）若是A关于x轴的对称点，设点，连接NA，直线NA与椭圆C相交于点E，直线与x轴相交于点M，求点M的坐标．

【题目】某国营企业集团公司现有员工1000名，平均每人每年创造利润10万元.为了激化内部活力，增强企业竞争力，集团公司董事会决定优化产业结构，调整出（）名员工从事第三产业；调整后，他们平均每人每年创造利润万元，剩下的员工平均每人每年创造的利润可以提高％.

（Ⅰ）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则最多调整出多少名员工从事第三产业？

（Ⅱ）在（1）的条件下，若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润，则实数的取值范围是多少？

【题目】圆：（）过点，离心率为，其左、右焦点分别为，，且过焦点的直线交椭圆于，.

（Ⅰ）求椭圆的方程；

（Ⅱ）若点的坐标为，设直线与直线的斜率分别为，试证明：.

【题目】如图，四棱锥中，底面为线段上一点，为的中点．

（1）证明：平面；

（2）求点到平面的距离．

【题目】已知椭圆的离心率为，右焦点为。斜率为1的直线与椭圆交于两点，以为底边作等腰三角形，顶点为。

（1）求椭圆的方程；

（2）求的面积。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网