题目内容
20.化简:$\frac{sinθ+sin2θ}{1+cosθ+cos2θ}$+$\frac{cosθ+sin2θ}{1+sinθ-cos2θ}$.分析 由条件利用同角三角函数的基本关系,二倍角公式化简所给的式子,可得结果.
解答 解:$\frac{sinθ+sin2θ}{1+cosθ+cos2θ}$+$\frac{cosθ+sin2θ}{1+sinθ-cos2θ}$=$\frac{sinθ+2sinθcosθ}{1+cosθ+{2cos}^{2}θ-1}$+$\frac{cosθ+2sinθcosθ}{1+sinθ-(1-{2sin}^{2}θ)}$
=$\frac{sinθ(1+2cosθ)}{cosθ(1+2cosθ)}$+$\frac{cosθ(1+2sinθ)}{sinθ(1+2sinθ)}$=tanθ+cotθ=$\frac{1}{sinθcosθ}$=$\frac{2}{sin2θ}$.
点评 本题主要考查同角三角函数的基本关系,二倍角公式的应用,属于基础题.

练习册系列答案
相关题目
13.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
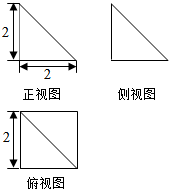

| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |