题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
,![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 为棱
为棱![]() 上的点,
上的点,![]() ,
,![]() .
.
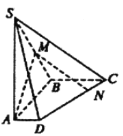
(1)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)在第(2)问条件下,设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求当
,求当![]() 取最大值时点
取最大值时点![]() 的位置.
的位置.
【答案】(1)证明见解析;(2)![]() ;(3)当
;(3)当![]() 最大时,点N在线段CD上,且
最大时,点N在线段CD上,且![]() .
.
【解析】
(1)取线段SC的中点E,根据中位线定理即可证明![]() ,因而得到AMED为平行四边形,即可证明
,因而得到AMED为平行四边形,即可证明![]() 平面SCD.
平面SCD.
(2)建立空间直角坐标系,写出各个点的坐标,因而可以求得平面AMC和平面SAB的法向量,利用法向量的数量积求得平面AMC与平面SAB所成的锐二面角的余弦值即可。
(3)设出N点坐标,利用直线与平面夹角的正弦值即为直线与平面法向量夹角的余弦值即可求得![]() 的表达式;根据基本不等式成立的条件,求得N点的坐标,即可判断出N点的位置。
的表达式;根据基本不等式成立的条件,求得N点的坐标,即可判断出N点的位置。
(1)证明:取线段SC的中点E,连接ME,ED.
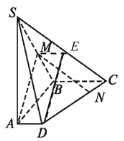
在![]() 中,ME为中位线,∴
中,ME为中位线,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形AMED为平行四边形.
∴![]() .
.
∵![]() 平面SCD,
平面SCD,![]() 平面SCD,
平面SCD,
∴![]() 平面SCD.
平面SCD.
(2)解:以点A为坐标原点,建立分别以AD、AB、AS为x轴、y轴、z轴,如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由条件得M为线段SB近B点的三等分点.
于是![]() ,即
,即![]()
设平面AMC的一个法向量为![]() ,则
,则 ,
,
将坐标代入得![]() ,
,
另外易知平面SAB的一个法向量为![]() ,
,
所以平面AMC与平面SAB所成的锐二面角的余弦为 .
.
(3)设![]() ,其中
,其中![]() .
.
由于![]() ,所以
,所以![]() .
.
所以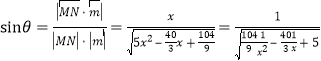 ,
,
可知当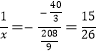 ,即
,即![]() 时分母有最小值,此时
时分母有最小值,此时![]() 有最大值,
有最大值,
此时,![]() ,即点N在线段CD上且
,即点N在线段CD上且![]() .
.

练习册系列答案
相关题目

