题目内容
【题目】下列说法错误的是
A. 相关关系是一种非确定性关系
B. 线性回归方程对应的直线
，至少经过其样本数据点
中的一个点
C. 在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高
D. 在回归分析中，
为
的模型比为
的模型拟合的效果好
【答案】B
【解析】
利用相关关系、回归直线、残差图以及相关指数的概念来进行判断。
对于选项A，相关关系是一种非确定的关系，而函数关系是一种确定的关系，A选项正确；
对于选项B，回归直线
过样本数据
的中心点
，并不一定过样本数据中的某一个点，B选项错误；
对于C选项，在残差图中，残差点分布的带状区域的宽度越狭窄，说明数据越逼近回归直线，两个变量的相关关系越强，其拟合精确度越高，C选项正确；
对于D选项而言，
越大，其拟合效果越好，D选项正确。
故选：B.
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
【题目】某种仪器随着使用年限的增加，每年的维护费相应增加. 现对一批该仪器进行调查，得到这批仪器自购入使用之日起，前5年平均每台仪器每年的维护费用大致如下表：
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 | 0.7 | 1.2 | 1.6 | 2.1 | 2.4 |
（1）根据表中所给数据，试建立
关于
的线性回归方程
；
（2）若该仪器的价格是每台12万元，你认为应该使用满五年换一次仪器，还是应该使用满八年换一次仪器？并说明理由.
参考公式：用最小二乘法求线性回归方程的系数公式：
,
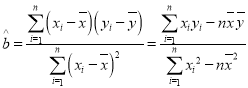【题目】据统计，2017年国庆中秋假日期间，黔东南州共接待游客590.23万人次，实现旅游收入48.67亿元，同比分别增长44.57%、55.22%.旅游公司规定：若公司导游接待旅客，旅游年总收入不低于40（单位：百万元），则称为优秀导游.经验表明，如果公司的优秀导游率越高，则该公司的影响度越高.已知甲、乙两家旅游公司各有导游100名，统计他们一年内旅游总收入，分别得到甲公司的频率分布直方图和乙公司的频数分布表如下：
分组 |
|
|
|
|
|
频数 |
| 18 | 49 | 24 | 5 |
（Ⅰ）求
的值，并比较甲、乙两家旅游公司，哪家的影响度高?
（Ⅱ）若导游的奖金
（单位：万元），与其一年内旅游总收入
（单位：百万元）之间的关系为
，求甲公司导游的年平均奖金；
（Ⅲ）从甲、乙两家公司旅游收入在
的总人数中，用分层抽样的方法随机抽取6人进行表彰，其中有两名导游代表旅游行业去参加座谈，求参加座谈的导游中有乙公司导游的概率.
【题目】某厂生产不同规格的一种产品，根据检测标准，其合格产品的质量
与尺寸x（mm）之间近似满足关系式
（b、c为大于0的常数）．按照某项指标测定，当产品质量与尺寸的比在区间
内时为优等品．现随机抽取6件合格产品，测得数据如下：
尺寸x（mm） | 38 | 48 | 58 | 68 | 78 | 88 |
质量y (g) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
（Ⅰ）现从抽取的6件合格产品中再任选3件，记
为取到优等品的件数，试求随机变量的分布列和期望；
（Ⅱ）根据测得数据作了初步处理，得相关统计量的值如下表：
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
（ⅰ）根据所给统计量，求y关于x的回归方程；
（ⅱ）已知优等品的收益
（单位：千元）与
的关系为
，则当优等品的尺寸x为何值时，收益的预报值最大？（精确到0.1）
附：对于样本
，其回归直线
的斜率和截距的最小二乘估计公式分别为：
，
，
.