题目内容
【题目】已知椭圆![]() 的长轴长为4,过点
的长轴长为4,过点![]() 且斜率为
且斜率为![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且点
两点,且点![]() 为线段
为线段![]() 的中点
的中点
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 为坐标原点,过右焦点
为坐标原点,过右焦点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,(
两点,(![]() 不在
不在![]() 轴上),求
轴上),求![]() 面积
面积![]() 的最大值.
的最大值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由已知条件推导出![]() ,设
,设![]()
![]() ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.
(2)设![]() ,由题意设直线AB的方程为
,由题意设直线AB的方程为![]() ,由
,由 ,得关于
,得关于![]() 的一元二次方程,由此韦达定理、点到直线距离公式等结合已知条件能求出
的一元二次方程,由此韦达定理、点到直线距离公式等结合已知条件能求出![]() 面积的最大值.
面积的最大值.
解:由题知,长轴长为4,即![]() ①,
①,
过点![]() 且斜率为
且斜率为![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ②,
②,![]() ③.
③.
②![]() ③得
③得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ④
④
由①④解得,![]() ,故椭圆C的标准方程为
,故椭圆C的标准方程为![]()
(2)由(1)知![]() ,则
,则![]() ,所以右焦点
,所以右焦点![]()
又因为过右焦点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,(
两点,(![]() 不在
不在![]() 轴上),
轴上),
设![]() ,由题意:
,由题意:
①当斜率不存时,设![]() 的方程为
的方程为![]()
则![]() ,
,![]()
②当斜率存时,设![]() 的方程为
的方程为![]() ,
,
由题意:
 ,消去
,消去![]() 并整理,得
并整理,得![]() ,
,
由韦达定理,得
点![]() 到直线
到直线![]() 的距离为
的距离为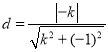 ,
,
![]()
![]()
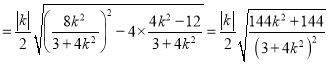
设![]() ,
,
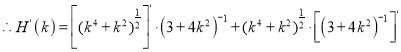
![]()
![]()
![]()
![]()
令![]() ,得
,得![]() ,又因为
,又因为![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 单调递增,
单调递增,
所以![]() 在
在![]()
![]() 没有极值.
没有极值.
所以当斜率不存时![]() 有极大值为
有极大值为![]() .
.
综上所述,![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
相关题目