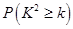题目内容
为了了解高一年级学生的身高情况,某校按10%的比例对全校800名高一年级学生按性别进行抽样检查,得到如下频数分布表:
表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190] |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:男生身高频数分布表
| 身高(cm) | [150,155) | [150,160) | [160,165) | [165,170) | [170,175) | [175,180] |
| 频数 | 2 | 12 | 16 | 6 | 3 | 1 |
(1)分别估计高一年级男生和女生的平均身高;
(2)在样本中,从身高180cm以上的男生中任选2人,求至少有一人身高在185cm以上的概率.
(1)174.75cm和162.375cm;(2)0.6.
解析试题分析:本题主要考查频率分布表、样本平均数、随机事件的概率等基础知识,考查分析问题解决问题的能力、计算能力.第一问,出现频率分布表或频率分布直方图后求样本平均数,利用公式“平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和”计算男生和女生的平均身高;第二问,将180cm以上的6人用字母表示出来,从6人中任选2人,写出所有情况,在所有情况中选出符合题意的种数,用这个数除以总的情况种数即可.
(1)设高一年级男生和女生的平均身高分别为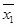 ,
,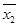 ,根据分布表,有
,根据分布表,有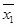 =
=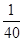 [(162.5+187.5)×2+167.5×5+172.5×14+177.5×13+182.5×4]=174.75,
[(162.5+187.5)×2+167.5×5+172.5×14+177.5×13+182.5×4]=174.75,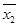 =
=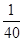 [152.5×2+157.5×12+162.5×16+167.5×6+172.5×3+177.5×1]=162.375.
[152.5×2+157.5×12+162.5×16+167.5×6+172.5×3+177.5×1]=162.375.
由此估计高一年级男生和女生的平均身高分别为174.75cm和162.375cm. 6分
(2)记样本中身高在[180,185)和[185,190]的男生分别为ai,bj,
i=1,2,3,4,j=1,2.
从这些男生中任选2人,共15种可能结果:
a1a2,a1a3,a1a4,a1b1,a1b2,a2a3,a2a4,a2b1,a2b2,a3a4,a3b1,a3b2,a4b1,a4b2,b1b2. 8分
其中求至少有一人身高在185cm以上的共9种可能结果:
a1b1,a1b2,a2b1,a2b2,a3b1,a3b2,a4b1,a4b2,b1b2. 10分
所求概率为P=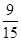 =0.6. 12分
=0.6. 12分
考点:频率分布表、样本平均数、随机事件的概率.

(12分)(2011•福建)某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X | 1 | 2 | 3 | 4 | 5 |
| f | a | 0.2 | 0.45 | b | c |
(Ⅱ)在(Ⅰ)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2,这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
已知某地每单位面积菜地年平均使用氮肥量x(kg)与每单位面积蔬菜年平均产量y(t)之间的关系有如下数据:
| 年份 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| x(kg) | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
| y(t) | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
| | ||||||||
| 年份 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | |
| x(kg) | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
| y(t) | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 | |
(2)若线性相关,求蔬菜产量y与使用氮肥量x之间的回归直线方程,并估计每单位面积施肥150 kg时,每单位面积蔬菜的年平均产量.
(已知数据:
 =101,
=101, ≈10.113 3,
≈10.113 3, =161 125,
=161 125, =1 628.55,
=1 628.55, =16 076.8)
=16 076.8) 
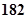 ;乙班10名同学,他们的身高(单位:cm)数据是
;乙班10名同学,他们的身高(单位:cm)数据是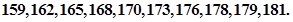

 名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为 ,女生数据的平均数为
,女生数据的平均数为 .
. ,
, 的值;
的值;
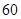 名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过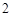 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过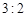 .
.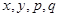 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).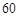 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定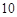 人,若需从这
人,若需从这 人进行问卷调查,设
人进行问卷调查,设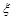 为选取的
为选取的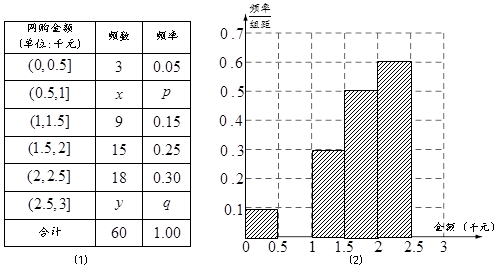

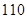 只海豚进行了检测,并将有关数据整理为不完整的
只海豚进行了检测,并将有关数据整理为不完整的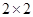 列联表,如表2.
列联表,如表2.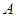 、
、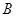 、
、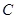 、
、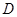 、
、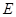 的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
的值,并判断有多大的把握认为海豚身体不健康与受到污染有关; 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有 人为环保专家的概率.
人为环保专家的概率.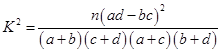 ,其中
,其中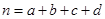 .
.