题目内容
给出下列四个命题:
①若| |+|
|+| |=0,则
|=0,则 =
= =
= ;
;
②在△ABC中,若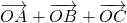 =
= ,则O为△ABC的重心;
,则O为△ABC的重心;
③若 ,
, 是共线向量,则
是共线向量,则 •
• =|
=| |•|
|•| |,反之也成立;
|,反之也成立;
④若 ,
, 是非零向量,则
是非零向量,则 +
+ =
= 的充要条件是存在非零向量
的充要条件是存在非零向量 ,使
,使 •
• +
+ •
• =
= .
.
其中,正确命题的个数是
- A.1
- B.2
- C.3
- D.4
B
分析:对于①,利用实数的性质即可进行判断;对于②,延长AO到E,使OE=AO,交BC于F,根据图形的对称性,欲证明O为△ABC的重心,只须证明AO所在的直线为△ABC的边BC上的中线即可,结合向量的几何意义,也就是要证明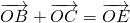 即可.对于③,利用向量的数量积公式即可进行判断;对于④,利用向量的数量积与垂直的关系进行判断即可.
即可.对于③,利用向量的数量积公式即可进行判断;对于④,利用向量的数量积与垂直的关系进行判断即可.
解答: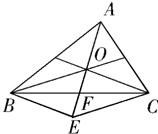 证明:①若|
证明:①若| |+|
|+| |=0,则|
|=0,则| |=|
|=| |=0,则
|=0,则 =
= =
= ;
;
正确;
对于②:如图,延长AO到E,
使OE=AO,交BC于F,
则 .
.
而由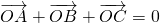 ,
,
有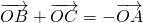 ,∴
,∴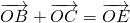 ,
,
∴四边形OBEC为平行四边形.
∴OE平分BC,即AO所在的直线为△ABC的边BC上的中线.
同理可证,CO,BO所在的直线分别为AB,AC边上的中线.∴O为△ABC的重心.正确;
对于③:若 ,
, 是共线向量,则它们的夹角θ为0或π,则
是共线向量,则它们的夹角θ为0或π,则 =|
=| |•|
|•| |cosθ=±|
|cosθ=±| |•|
|•| |,故③错;
|,故③错;
④若 ,
, 是非零向量,若存在非零向量
是非零向量,若存在非零向量 ,使
,使 •
• +
+ •
• =(
=( +
+ )•
)• =0,说明向量(
=0,说明向量( +
+ )与
)与 垂直,并不能得出
垂直,并不能得出 +
+ =
= ,故错.
,故错.
故选B.
点评:本小题主要考查三角形重心、三角形重心的应用、向量加法的几何意义、向量的数量积等基础知识,考查运算求解能力、转化思想.属于基础题.
分析:对于①,利用实数的性质即可进行判断;对于②,延长AO到E,使OE=AO,交BC于F,根据图形的对称性,欲证明O为△ABC的重心,只须证明AO所在的直线为△ABC的边BC上的中线即可,结合向量的几何意义,也就是要证明
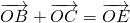 即可.对于③,利用向量的数量积公式即可进行判断;对于④,利用向量的数量积与垂直的关系进行判断即可.
即可.对于③,利用向量的数量积公式即可进行判断;对于④,利用向量的数量积与垂直的关系进行判断即可.解答:
 证明:①若|
证明:①若| |+|
|+| |=0,则|
|=0,则| |=|
|=| |=0,则
|=0,则 =
= =
= ;
;正确;
对于②:如图,延长AO到E,
使OE=AO,交BC于F,
则
 .
.而由
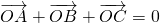 ,
,有
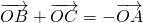 ,∴
,∴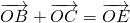 ,
,∴四边形OBEC为平行四边形.
∴OE平分BC,即AO所在的直线为△ABC的边BC上的中线.
同理可证,CO,BO所在的直线分别为AB,AC边上的中线.∴O为△ABC的重心.正确;
对于③:若
 ,
, 是共线向量,则它们的夹角θ为0或π,则
是共线向量,则它们的夹角θ为0或π,则 =|
=| |•|
|•| |cosθ=±|
|cosθ=±| |•|
|•| |,故③错;
|,故③错;④若
 ,
, 是非零向量,若存在非零向量
是非零向量,若存在非零向量 ,使
,使 •
• +
+ •
• =(
=( +
+ )•
)• =0,说明向量(
=0,说明向量( +
+ )与
)与 垂直,并不能得出
垂直,并不能得出 +
+ =
= ,故错.
,故错.故选B.
点评:本小题主要考查三角形重心、三角形重心的应用、向量加法的几何意义、向量的数量积等基础知识,考查运算求解能力、转化思想.属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目