题目内容
12、已知a、b是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:
①若a⊥α,a⊥β,则α∥β;
②若α⊥γ,β⊥γ,则α∥β;
③若α∥β,a?α,b?β,则a∥b;
④若α∥β,α∩γ=a,β∩γ=b,则a∥b.
其中正确命题的序号有
①若a⊥α,a⊥β,则α∥β;
②若α⊥γ,β⊥γ,则α∥β;
③若α∥β,a?α,b?β,则a∥b;
④若α∥β,α∩γ=a,β∩γ=b,则a∥b.
其中正确命题的序号有
①④
.分析:对于①若a⊥α,a⊥β,则α∥β;垂直于同一直线的两平面平行,正确.
对于②若α⊥γ,β⊥γ,则α∥β;垂直于一个平面的两个平面也有可能垂直,故错误
对于③若α∥β,a?α,b?β,则a∥b;两平面平行并不能推出平面里的直线平行.故错误.
对于④若α∥β,α∩γ=a,β∩γ=b,则a∥b.面面平行,被第三平面截得的两条直线平行,故正确.即可得到答案.
对于②若α⊥γ,β⊥γ,则α∥β;垂直于一个平面的两个平面也有可能垂直,故错误
对于③若α∥β,a?α,b?β,则a∥b;两平面平行并不能推出平面里的直线平行.故错误.
对于④若α∥β,α∩γ=a,β∩γ=b,则a∥b.面面平行,被第三平面截得的两条直线平行,故正确.即可得到答案.
解答:解:因为已知a、b是两条不重合的直线,α、β、γ是三个两两不重合的平面,
①若a⊥α,a⊥β,则α∥β;因为垂直于同一直线的两平面平行,显然①正确;
②若α⊥γ,β⊥γ,则α∥β;设α,β,γ分别是坐标平面,即可验证错误.
③若α∥β,a?α,b?β,则a∥b;a、b也可异面,显然③错误.
④若α∥β,α∩γ=a,β∩γ=b,则a∥b.由面面平行性质知,a∥b,故④正确.
故答案为①④.
①若a⊥α,a⊥β,则α∥β;因为垂直于同一直线的两平面平行,显然①正确;
②若α⊥γ,β⊥γ,则α∥β;设α,β,γ分别是坐标平面,即可验证错误.
③若α∥β,a?α,b?β,则a∥b;a、b也可异面,显然③错误.
④若α∥β,α∩γ=a,β∩γ=b,则a∥b.由面面平行性质知,a∥b,故④正确.
故答案为①④.
点评:此题主要考查平面与平面平行的性质,属于概念性质理解的问题,题目比较简单且无计算量,属于基础题目.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
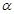 ,
,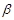 是两个不重合的平面,下列命题中正确的是( )
是两个不重合的平面,下列命题中正确的是( )
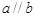 ,
,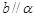 ,则
,则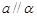
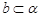 ,
,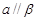 ,
,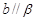 ,则
,则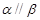
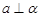 ,
,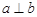
 ,且
,且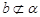 时,若
时,若 ∥
∥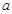 ∥
∥