题目内容
在等差数列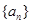 中,
中,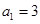 ,其前n项和为
,其前n项和为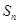 ,等比数列
,等比数列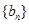 的各项均为正数,
的各项均为正数,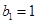 ,公比为q,且
,公比为q,且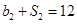 ,
,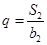 .
.
(1)求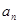 与
与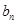 ;
;
(2)设数列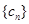 满足
满足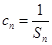 ,求
,求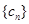 的前n项和
的前n项和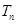 .
.
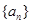 中,
中,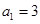 ,其前n项和为
,其前n项和为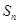 ,等比数列
,等比数列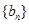 的各项均为正数,
的各项均为正数,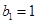 ,公比为q,且
,公比为q,且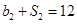 ,
,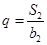 .
.(1)求
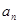 与
与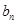 ;
;(2)设数列
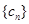 满足
满足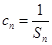 ,求
,求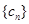 的前n项和
的前n项和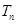 .
.(1) ,
, ;(2)
;(2) .
.
 ,
, ;(2)
;(2) .
.试题分析:本题主要考查等差数列的通项公式、等比数列的通项公式、等差数列的前n项和公式、裂项相消法求和等数学知识,考查学生的计算能力和分析问题的能力.第一问,利用等比数列的通项公式和等差数列的前n项和公式将已知表达式展开,求出
 和
和 ,从而求出等差数列、等比数列的通项公式;第二问,利用等差数列的前n项和公式先求出
,从而求出等差数列、等比数列的通项公式;第二问,利用等差数列的前n项和公式先求出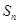 ,得到
,得到 进行裂项,用裂项相消法求数列的前n项和
进行裂项,用裂项相消法求数列的前n项和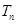 .
.试题解析:(1)设
 的公差为
的公差为 .
.因为
 所以
所以 3分
3分解得
 或
或 (舍),
(舍),
故
 ,
, . 6分
. 6分(2)由(1)可知,
 , 7分
, 7分所以
 . 9分
. 9分故
 12分
12分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
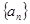 是等差数列,前n项和是
是等差数列,前n项和是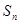 ,且
,且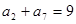 ,
,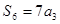 ,
,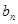 =
=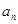 ·2n,求数列
·2n,求数列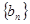 的前n项和
的前n项和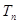

 的前n项和为Sn,若S2n+1-Sn≤
的前n项和为Sn,若S2n+1-Sn≤ 对n∈N*恒成立,则正整数m的最小值为________.
对n∈N*恒成立,则正整数m的最小值为________. 是公差不为零的等差数列,并且
是公差不为零的等差数列,并且 是等比数列
是等比数列 的相邻三项,若
的相邻三项,若 ,则
,则 等于( )
等于( )



 (S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(S2n+S2m)-(n-m)2,其中m,n为任意正整数. -
- an+33=k2的所有正整数k,n.
an+33=k2的所有正整数k,n.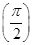 =0.
=0.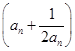 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.