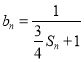题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)设函数![]() 若至少存在一个
若至少存在一个![]() ,使得
,使得![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求导后代入![]() 求得
求得![]() 在
在![]() 处的切线斜率,再利用点斜式求得切线方程即可.
处的切线斜率,再利用点斜式求得切线方程即可.
(2)求导后分![]() 与
与![]() 时,分析单调性再根据函数性质的最值满足的条件列式求不等式即可.
时,分析单调性再根据函数性质的最值满足的条件列式求不等式即可.
(1)当![]() 时,
时,![]() ,
,
∴![]() ,即切线斜率为2,故由点斜式方程可得切线方程为
,即切线斜率为2,故由点斜式方程可得切线方程为![]() ,即
,即![]()
(2)原问题等价于至少存在一个![]() ,使得
,使得![]() 成立,
成立,
令![]() ,
,![]() 则
则![]() ,
,
①当![]() 时,
时,![]() ,则函数h(x)在[1,e]上单调递减,故h(x)min=h(e)=﹣2<0,符合题意;
,则函数h(x)在[1,e]上单调递减,故h(x)min=h(e)=﹣2<0,符合题意;
②当![]() 时,令,
时,令,![]() ,解得
,解得![]() ,则函数h(x)在
,则函数h(x)在![]() 上单调递减,令
上单调递减,令![]() ,解得
,解得![]() ,则函数h(x)在
,则函数h(x)在![]() 单调递增,
单调递增,
且![]() ,
,![]() ,
,![]()
1.当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,
,![]() 单调递增,
单调递增,
此时![]() 不符合题意
不符合题意
2.当![]() ,即
,即![]() 时, 在
时, 在![]() 上
上![]() ,
,![]() 单调递减,
单调递减,
此时![]() 满足题意
满足题意
3.当![]() ,即
,即![]() 时,
时,![]() ,不满足题意
,不满足题意
综上,实数a的取值范围为![]() .
.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目