题目内容
【题目】![]() 是定义在区间
是定义在区间![]() 上且同时满足如下条件的函数
上且同时满足如下条件的函数![]() 所组成的集合:
所组成的集合:
①对任意的![]() ,都有
,都有![]() ;
;
②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]()
(1)设![]() ,试判断
,试判断![]() 是否属于集合
是否属于集合![]() ;
;
(2)若![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,求证:满足条件的
,求证:满足条件的![]() 是唯一的;
是唯一的;
(3)设![]() ,且
,且![]() ,试求参数
,试求参数![]() 的取值范围
的取值范围
【答案】(1)是![]() 的元素;(2)证明见解析;(3)
的元素;(2)证明见解析;(3)![]()
【解析】
(1)构造函数f(x)=φ(x)![]() x
x![]() x2
x2![]() x+1,判断单调性求最值即可证明
x+1,判断单调性求最值即可证明
(2)要证明唯一性通过反证法来证明,假设满足这样条件的x0有两个,导出矛盾.
(3)转化为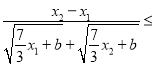 c(x2﹣x1)恒成立,利用单调性求最值求解
c(x2﹣x1)恒成立,利用单调性求最值求解
(1)x∈[1,2],所以φ(x)∈(![]() ,
,![]() )
)
令f(x)=φ(x)![]() x
x![]() x2
x2![]() x+1,则f'(x)
x+1,则f'(x)![]() x
x![]() ,
,
因为x∈[1,2],所以f'(x)≤0,所以f(x)在[1,2]上单调递减,
对任意1≤x1≤x2≤2,f(x1)≤f(x2)φ(x2)﹣φ(x1)![]() (x2﹣x1)|φ(x1)﹣φ(x2)|
(x2﹣x1)|φ(x1)﹣φ(x2)|![]() |x1﹣x2|,即存在
|x1﹣x2|,即存在![]()
所以φ(x)∈A.
(2)假设存在不同的两个数a、b∈(1,2),使得φ(a)=a,φ(b)=b,
因为φ(x)∈A,所以|φ(a)﹣φ(b)|=|a﹣b|≤c|a﹣b|,
因为a≠b,所以|a﹣b|>
所以满足x0=φ(x0)的x0是唯一的.
(3)因为φ(x)单调递增,故φ(x)∈(1,2),所以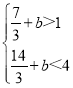 ,解得b∈(
,解得b∈(![]() ,
,![]() );
);
对任意1≤x1≤x2≤2,|φ(x1)﹣φ(x2)|![]()
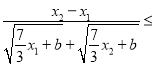 c(x2﹣x1)
c(x2﹣x1)
所以![]() 对任意1≤x1≤x2≤2恒成立,
对任意1≤x1≤x2≤2恒成立,
所以![]() b
b![]() .
.
综上b∈(![]() ,
,![]() ).
).

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002,…,800进行编号.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42.
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
| 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
①若在该样本中,数学成绩优秀率是30%,求a,b的值:
②在地理成绩及格的学生中,已知![]() 求数学成绩优秀的人数比及格的人数少的概率.
求数学成绩优秀的人数比及格的人数少的概率.