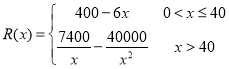题目内容
【题目】已知曲线![]() 的方程为
的方程为![]() ,过原点作斜率为
,过原点作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,……,如此下去,一般地,过
,……,如此下去,一般地,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,设点
,设点![]() .
.
(1)指出![]() ,并求
,并求![]() 与
与![]() 的关系式
的关系式![]() ;
;
(2)求![]() 的通项公式,并指出点列
的通项公式,并指出点列![]() ,
,![]() ,……,
,……,![]() ,……向哪一点无限接近?说明理由;
,……向哪一点无限接近?说明理由;
(3)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,设
,设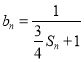 ,求所有可能的乘积
,求所有可能的乘积![]() 的和.
的和.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;向点
;向点![]() 无限接近;(3)
无限接近;(3)![]() .
.
【解析】
(1)设点![]() ,则点
,则点![]() ,利用曲线的相交关系,联立方程组求解,即可得出结果;
,利用曲线的相交关系,联立方程组求解,即可得出结果;
(2)先由(1)的结果,得到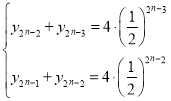 ,推出
,推出![]() ,再由累加法,即可求出通项公式;求数列的极限,结合双曲线的方程,即可求出无限接近的点;
,再由累加法,即可求出通项公式;求数列的极限,结合双曲线的方程,即可求出无限接近的点;
(3)先由(2)得到![]() ,求出
,求出![]() ,利用矩阵研究,根据等比数列的求和公式,以及分组求和的方法,即可求出结果.
,利用矩阵研究,根据等比数列的求和公式,以及分组求和的方法,即可求出结果.
(1)由题意得,![]() ,设点
,设点![]() ,则点
,则点![]() ,
,
由题意得 ,所以
,所以![]() ;
;
(2)分别用![]() 、
、![]() 代换
代换![]() 中的
中的![]() ,得
,得
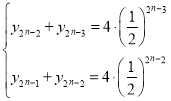 ,解得:
,解得:![]() ,
,
所以![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,
以上各式相加得: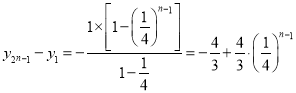 ,
,
又![]() ,所以
,所以![]() ,
,![]() ;
;
因为 ,由
,由![]() 代入
代入![]() 可得:
可得:![]() ;
;
所以点列![]() ,
,![]() ,……,
,……,![]() ,……向点
,……向点![]() 无限接近;
无限接近;
(3)因为![]() ,所以其前
,所以其前![]() 项和
项和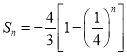 ,
,
因此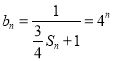 ,
,![]() ,
,
将所得的积排成如下矩阵: ,
,
设矩阵![]() 的各项和为
的各项和为![]() .
.
在矩阵的左下方补上相应的数可得: ,
,
矩阵![]() 中第一行的各数和
中第一行的各数和![]() ,
,
矩阵![]() 中第二行的各数和
中第二行的各数和![]() ,
,
……
矩阵![]() 中第
中第![]() 行的各数和
行的各数和![]() ,
,
从而矩阵![]() 中所有数之和为
中所有数之和为
![]()
![]() ;
;
因此,所有可能的乘积![]() 的和为:
的和为:
![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目