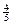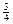题目内容
甲、乙两船驶向一个不能同时停泊两艘船的码头，它们在一昼夜内到达该码头的时刻是等可能的，如果甲船停泊时间为1h，乙船停泊时间为2h，求它们中的任意一艘都不需要等待码头空出的概率．
这是一个几何概率问题，如图，设甲、乙两艘船到达码头的时刻分别为x和y，A为“两船都需要等待码头空出”，则0≤x≤24,0≤y≤24，且基本事件空间为{Ω|(x,y)|x∈［0,24］,y∈［0,24］}．
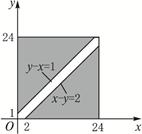
要使两船都不需要等待码头空出，当且仅当甲比乙早到达1h以上或乙比甲早到达2h以上，
即y-x≥1或x-y≥2.
故A={(x,y)|y-x≥1或x-y≥2,?x∈［0,24］,y∈［0,24］}．
A为图中阴影部分，Ω为边长是24的正方形，由几何概率定义，知所求概率为
P(A)=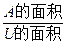
=
=
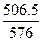="0.879" 34．
要使两船都不需要等待码头空出，当且仅当甲比乙早到达1h以上或乙比甲早到达2h以上，
即y-x≥1或x-y≥2.
故A={(x,y)|y-x≥1或x-y≥2,?x∈［0,24］,y∈［0,24］}．
A为图中阴影部分，Ω为边长是24的正方形，由几何概率定义，知所求概率为
P(A)=
=
=
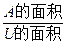
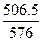="0.879" 34．问题的关键是要构造出随机事件对应的几何图形，利用图形的几何度量来求随机事件的概率．
练习册系列答案
相关题目
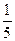
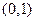中随机地取出两个数，求两数之和小于
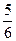的概率。
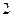的正方形木板，上面画有抛物线型的图案（阴影部分），某人向此板投镖，假设每次都能击中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是（ ）
