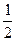题目内容
将长为l的棒随机折成3段,求3段构成三角形的概率.

设A=“3段构成三角形”,x,y分别表示其中两段的长度,则第3段的长度为l-x-y.
则试验的全部结果可构成集合
 ={(x,y)|0<x<l,0<y<l,0<x+y<l},
={(x,y)|0<x<l,0<y<l,0<x+y<l},
要使3段构成三角形,当且仅当任意两段之和大于第3段,即x+y>l-x-y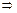 x+y>
x+y>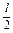 ,x+l-x-y>y
,x+l-x-y>y
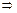 y<
y<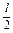 ,y+l-x-y>x
,y+l-x-y>x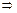 x<
x<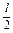 .
.
故所求结果构成集合
A= .
.
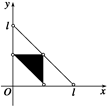
由图可知,所求概率为
P(A)= =
= =
= .
.

则试验的全部结果可构成集合
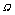 ={(x,y)|0<x<l,0<y<l,0<x+y<l},
={(x,y)|0<x<l,0<y<l,0<x+y<l},要使3段构成三角形,当且仅当任意两段之和大于第3段,即x+y>l-x-y
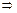 x+y>
x+y>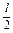 ,x+l-x-y>y
,x+l-x-y>y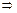 y<
y<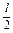 ,y+l-x-y>x
,y+l-x-y>x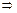 x<
x<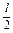 .
.故所求结果构成集合
A=
 .
.由图可知,所求概率为
P(A)=
 =
= =
= .
.
练习册系列答案
相关题目



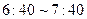 之间把报纸送到家,若小王每天在
之间把报纸送到家,若小王每天在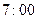 准时离家上班,则小王离家前能拿到报纸的概率( )
准时离家上班,则小王离家前能拿到报纸的概率( )
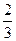
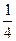
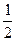
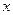 的一元二次函数
的一元二次函数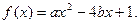 (Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
(Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为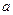 和
和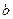 ,求函数
,求函数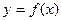 在区间[
在区间[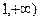 上是增函数的概率;(Ⅱ)设点(
上是增函数的概率;(Ⅱ)设点(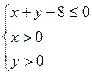 内的随机点,求函数
内的随机点,求函数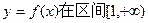 上是增函数的概率。
上是增函数的概率。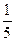 B
B 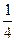 C
C  D
D