题目内容
(1)由“若 则
则 ”类比“若
”类比“若 为三个向量则
为三个向量则 ”
”
(2)在数列 中,
中, 猜想
猜想
(3)在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”
(4)已知 ,则
,则 .
.
上述四个推理中,得出的结论正确的是____ .(写出所有正确结论的序号)
(2)(3)
解析考点:类比推理;归纳推理.
分析:向量不符合结合律,通过配凑做出数列的通项,四面体的任意三个面的面积之和大于第四面的面积,当给x赋值1时,可以得到各项的系数之和,但是不同的符号不正确.
解:向量不符合结合律,知道(1)不正确,
∵an+1=2an+2
∴2+an+1=2(an+2)
∴{an+2}是一个等比数列,
∴an=2n-2,故(2)正确,
根据在平面内“三角形的两边之和大于第三边”类比在空间中
“四面体的任意三个面的面积之和大于第四面的面积,(3)正确.
当给x赋值1时,可以得到各项的系数之和,但是不同的符号不正确,故(4)不正确,
故答案为:(2)(3)

练习册系列答案
相关题目
 在
在
 内,则有结论
内,则有结论  ,把命题类比推广到空间,若点
,把命题类比推广到空间,若点 内,则有结论:
内,则有结论:  ,试证明
,试证明 至少有一个不小于1.
至少有一个不小于1. 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 ;②
;② 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明) ,函数
,函数 不是等比源函数;
不是等比源函数; ,函数
,函数 都是等比源函数.
都是等比源函数.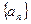 中,有
中,有 成立.
成立. 中,
中, _______________成立. Ks
_______________成立. Ks ,使得
,使得 ”是真命题,
”是真命题, 则实数
则实数 的取值范围是
的取值范围是  中,若
中,若 ,则有等式
,则有等式 (
( ,
, )成立.类比上述性质,相应地,在等比数列
)成立.类比上述性质,相应地,在等比数列 中,若
中,若 ,则有等式 成立.
,则有等式 成立. 块区域,可数得
块区域,可数得 ,则
,则