[题目]点P是棱长为1的正方体ABCD﹣A1B1C1D1的底面A1B1C1D1上一点.则的取值范围是 . 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】点P是棱长为1的正方体ABCD﹣A1B1C1D1的底面A1B1C1D1上一点，则的取值范围是__.

【答案】[﹣，0]

【解析】

建立空间直角坐标系，设出点P的坐标为（x，y，z），则由题意可得0≤x≤1，0≤y≤1，z＝1，计算x2﹣x，利用二次函数的性质求得它的值域即可．

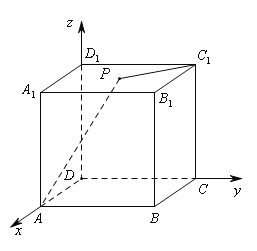
解：以点D为原点，以DA所在的直线为x轴，以DC所在的直线为y轴，以DD1所在的直线为z轴，

建立空间直角坐标系，如图所示；

则点A（1，0，0），C1 （0，1，1），

设点P的坐标为（x，y，z），由题意可得 0≤x≤1，0≤y≤1，z＝1；

∴（1﹣x，﹣y，﹣1），（﹣x，1﹣y，0），

∴x（1﹣x）﹣y（1﹣y）+0＝x2﹣x+y2﹣y，

由二次函数的性质可得，当x＝y时，取得最小值为；

当x＝0或1，且y＝0或1时，取得最大值为0，

则的取值范围是[，0]．

故答案为：[，0]．

练习册系列答案

相关题目

【题目】设是定义在上的函数，若对任何实数以及中的任意两数、，恒有，则称为定义在上的函数．

（1）证明函数是定义域上的函数；

（2）判断函数是否为定义域上的函数，请说明理由；

（3）若是定义域为的函数，且最小正周期为，试证明不是上的函数．

【题目】对同学们而言，冬日的早晨离开暖融融的被窝，总是一个巨大的挑战，而咬牙起床的唯一动力，就是上学能够不迟到．己知学校要求每天早晨7:15之前到校，7:15之后到校记为迟到．小明每天6:15会被妈妈叫醒起味，吃早餐、洗漱等晨间活动需要半个小时，故每天6:45小明就可以出门去上学．从家到学校的路上，若小明选择步行到校，则路上所花费的时间相对准确，若以随机变量（分钟）表示步行到校的时间，可以认为．若小明选择骑共享单车上学，虽然骑行速度快于步行，不过由于车况、路况等不确定因素，路上所需时间的随机性增加，若以随机变量（分钟）描述骑车到校的时间，可以认为．若小明选择坐公交车上学，速度很快，但是由于等车时间、路况等不确定因素，路上所需时间的随机性进一步增加，若以随机变量（分钟）描述坐公交车到校所需的时间，则可以认为．

（1）若某天小明妈妈出差没在家，小明一觉醒来已经是6:40了，他抓紧时间洗漱更衣，没吃早饭就出发了，出门时候是6:50．请问，小明是否有某种出行方案，能够保证上学不迟到？小明此时的最优选择是什么？

（2）已知共享单车每20分钟收费一元，若小明本周五天都骑共享单车上学，以随机变量表示这五天小明上学骑车的费用，求的期望与方差（此小题结果均保留三位有效数字）

已知若随机变量，则％，％，％．

【题目】给定整数，数列、、、每项均为整数，在中去掉一项，并将剩下的数分成个数相同的两组，其中一组数的和与另外一组数的和之差的最大值记为. 将、、、中的最小值称为数列的特征值.

（Ⅰ）已知数列、、、、，写出、、的值及的特征值；

（Ⅱ）若，当，其中、且时，判断与的大小关系，并说明理由；

（Ⅲ）已知数列的特征值为，求的最小值.

【题目】定义max{x1，x2，x3，…，xn}表示x1，x2，x3，…，xn中的最大值.已知数列an=，bn=，cn=，其中n+m+p=200，m=kn，n，m，p，k∈N*.记dn=max{an，bn，cn}

（Ⅰ）求max{an，bn}

（Ⅱ）当k=2时，求dn的最小值；

（Ⅲ）k∈N*，求dn的最小值.

【题目】某地拟规划种植一批芍药，为了美观，将种植区域（区域I）设计成半径为1km的扇形，中心角（）.为方便观赏，增加收入，在种植区域外围规划观赏区（区域II）和休闲区（区域III），并将外围区域按如图所示的方案扩建成正方形，其中点，分别在边和上．已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.