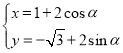题目内容
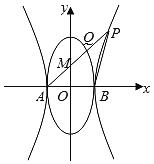
【题目】如图,椭圆![]() 的左、右顶点分别为A、B,双曲线
的左、右顶点分别为A、B,双曲线![]() 以A、B为顶点,焦距为
以A、B为顶点,焦距为![]() ,点P是
,点P是![]() 上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为
上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为![]()
![]() 为坐标原点.
为坐标原点.
(1)求双曲线![]() 的方程;
的方程;
(2)求点M的纵坐标![]() 的取值范围;
的取值范围;
(3)是否存在定直线![]() 使得直线BP与直线OM关于直线
使得直线BP与直线OM关于直线![]() 对称?若存在,求直线
对称?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在直线
;(3)存在直线![]() 满足题意,详见解析
满足题意,详见解析
【解析】
(1)根据题意,得到![]() ,即可求得双曲线
,即可求得双曲线![]() 的方程;
的方程;
(2)由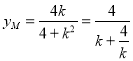 在
在![]() 上单调递增,即可求得点
上单调递增,即可求得点![]() 的纵坐标
的纵坐标![]() 的取值范围;
的取值范围;
(3)求出![]() ,可得直线
,可得直线![]() 与
与![]() 关于直线
关于直线![]() 对称,即可求解.
对称,即可求解.
(1)由题意,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,双曲线
,双曲线![]() 以A、B为顶点,焦距为
以A、B为顶点,焦距为![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
所以双曲线![]() 的方程
的方程![]() .
.
(2)由题意,设![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
代入椭圆方程,整理![]() ,
,
所以![]() 或
或![]() ,所以
,所以![]() ,
,
所以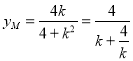 在
在![]() 上单调递增,所以
上单调递增,所以![]() .
.
(3)由(1)双曲线![]() 的方程
的方程![]() ,
,
可得![]() ,同理
,同理![]() ,
,
所以![]() ,即
,即![]() ,
,
设直线![]() ,则直线
,则直线![]() ,解得
,解得![]() ,
,
所以直线![]() 与
与![]() 关于直线
关于直线![]() 对称.
对称.

练习册系列答案
相关题目