题目内容
对于无穷数列 和函数
和函数 ,若
,若 ,则称
,则称 是数列
是数列 的母函数.
的母函数.
(Ⅰ)定义在 上的函数
上的函数 满足:对任意
满足:对任意 ,都有
,都有 ,且
,且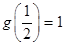 ;又数列
;又数列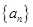 满足:
满足: .
.
求证:(1) 是数列
是数列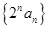 的母函数;
的母函数;
(2)求数列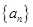 的前项
的前项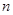 和
和 .
.
(Ⅱ)已知 是数列
是数列 的母函数,且
的母函数,且 .若数列
.若数列 的前
的前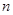 项和为
项和为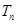 ,求证:
,求证: .
.
(Ⅰ)(1) 由题知 ,
,

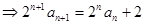 ,
,
 是数列
是数列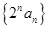 的母函数
的母函数
(2)  (Ⅱ)
(Ⅱ)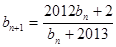 ,
, ,
,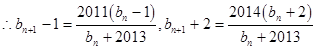
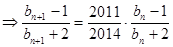 从而
从而 是以
是以 为首项,
为首项,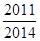 为公比的等比数列
为公比的等比数列
又 故当
故当 时,有
时,有
 ,化简得结论
,化简得结论
解析试题分析:(Ⅰ)(1)由题知 ,且
,且

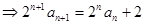 .
.
 是数列
是数列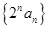 的母函数;
的母函数;
(2) 由(1) 知: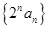 是首项和公差均为
是首项和公差均为 的等差数列,故
的等差数列,故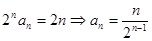 .
. ①
① ②
②
①-②得: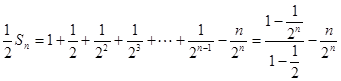
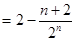 .
.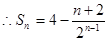 .
.
(Ⅱ)由题知: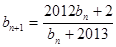 ,
, .
. 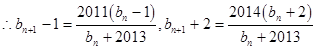
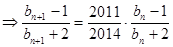 .
.
从而 是以
是以 为首项,
为首项,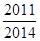 为公比的等比数列.
为公比的等比数列. .
.
又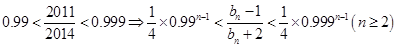
故当 时,有:
时,有:

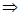
 .
.
考点:信息题及数列求和
点评:求解本题首先要正确理解所给信息母函数的实质,将其性质代入相应的函数式中推理;第一问的数列求和用到了错位相减法,这种方法是数列求和题常用到的方法,其适用于通项公式为关于n的一次函数式与指数式的乘积形式的数列

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 ,数列
,数列 满足
满足 。
。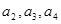 ;
;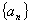 中,
中,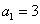 ,满足
,满足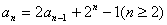 。
。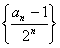 为等差数列;
为等差数列;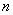 项和
项和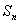 .
. ,
, 满足:
满足: .
.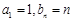 ,求数列
,求数列 ,且
,且 .
. ,求证:数列
,求证:数列 为等差数列;
为等差数列; 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项 应满足的条件.
应满足的条件.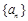 的前
的前 项和为
项和为 ,
, ,
, ,
,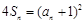 ,
, .
.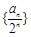 的前
的前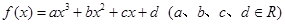 为奇函数,且在点
为奇函数,且在点 的切线方程为
的切线方程为
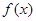 的表达式;
的表达式; 的各项都是正数,且对于
的各项都是正数,且对于 ,都有
,都有 ,求数列
,求数列 和通项公式;
和通项公式; 满足
满足 ,求数列
,求数列 的前
的前 项和为
项和为 ,且方程
,且方程 有一个根为
有一个根为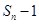 ,
, .
.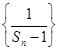 是等差数列;
是等差数列;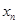 ,数列
,数列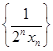 的前
的前 ,求
,求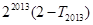 的值;
的值;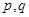 ,使得
,使得 ,
, ,
, 成等比数列,若存在,求出满足条件的
成等比数列,若存在,求出满足条件的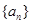 为等比数列,
为等比数列,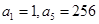 ;
;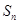 为等差数列
为等差数列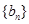 的前n项和,
的前n项和,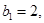
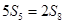 .
.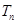
 ,求
,求 中,
中,
 ,求数列
,求数列 的前n项和
的前n项和 .
.