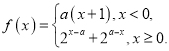题目内容
【题目】已知某工厂每天的固定成本是4万元,每生产一件产品成本增加100元,工厂每件产品的出厂价定为a元时,生产x件产品的销售收入为![]() (元),
(元),![]() 为每天生产x件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件a元进货后又以每件b元销售,
为每天生产x件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件a元进货后又以每件b元销售,![]() ,其中c为最高限价
,其中c为最高限价![]() ,
,![]() 为该产品畅销系数.据市场调查,
为该产品畅销系数.据市场调查,![]() 由当
由当![]() 是
是![]() 的比例中项时来确定.
的比例中项时来确定.
(1)每天生产量x为多少时,平均利润![]() 取得最大值?并求出
取得最大值?并求出![]() 的最大值;
的最大值;
(2)求畅销系数![]() 的值;
的值;
(3)若![]() ,当厂家平均利润最大时,求a与b的值.
,当厂家平均利润最大时,求a与b的值.
【答案】(1)每天生产量为400件时平均利润最大,最大值为200元;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)先求出总利润=![]() ,依据(平均利润=总利润/总产量)可得
,依据(平均利润=总利润/总产量)可得![]() ,利用均值不等式得最大利润;
,利用均值不等式得最大利润;
(2)由已知得![]() ,结合比例中项的概念可得
,结合比例中项的概念可得![]() ,两边同时除以
,两边同时除以![]() 将等式化为
将等式化为![]() 的方程,解出方程即可;
的方程,解出方程即可;
(3)利用![]() 平均成本
平均成本![]()
![]() 平均利润
平均利润![]() ,结合厂家平均利润最大时(由(1)的结果)可得
,结合厂家平均利润最大时(由(1)的结果)可得![]() 的值,利用
的值,利用![]() 可得
可得![]() 的值.
的值.
(1)由题意得,总利润为![]() .
.
于是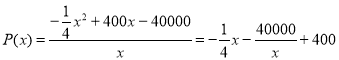
![]()
当且仅当![]() 即
即![]() 时等号成立.
时等号成立.
故每天生产量为400件时平均利润最大,最大值为200元.
(2)由![]() 可得
可得![]() ,
,
由![]() 是
是![]() 的比例中项可知
的比例中项可知![]() ,
,
即![]()
化简得![]() ,解得
,解得![]() .
.
(3)厂家平均利润最大,生产量为![]() 件.
件.
![]() .
.
(或者![]() )
)
代入![]() 可得
可得![]() .
.
于是![]() ,
,![]() .
.

练习册系列答案
相关题目