题目内容
设变量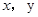 满足
满足 ,则
,则 的最大值为 ( )
的最大值为 ( )
A.  | B. | C. | D. |
B
解析试题分析:画出不等|x-2|+|y-2|≤1表示的可行域,表示以 A(1,2),B(2,1),C(3,2),D(2,3)为顶点的正方形及其内部。是一个正方形,得.
当x=1,y=2时,则 ;当x=2,y=1时,则
;当x=2,y=1时,则 ;
;
当x=3,y=2时,则 ;当x=2,y=3时,则
;当x=2,y=3时,则 ,
,
所以 的最大值为
的最大值为 。
。
考点:柯西不等式的几何意义。
点评:在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域;②求出可行域各个角点的坐标;③将坐标逐一代入目标函数;④验证,求出最优解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列坐标对应的点中,落在不等式 表示的平面区域内的是
表示的平面区域内的是
| A.(0,0) | B.(2,4) | C.(-1,4) | D.(1,8) |
设 为坐标原点,
为坐标原点, ,若
,若 满足
满足 ,则
,则 的最大值为
的最大值为
| A.4 | B.6 | C.8 | D.10 |
已知点 满足
满足 ,目标函数
,目标函数 仅在点(1,0)处取得最小值,则
仅在点(1,0)处取得最小值,则 的范围为( )
的范围为( )
A. | B. | C. | D. |
设m>1,在约束条件 目标函数z=x+my的最大值大于2,则m的取值范围为
目标函数z=x+my的最大值大于2,则m的取值范围为
A. | B. | C.(1,3) | D. |
若变量 满足约束条件
满足约束条件 ,
, ,则
,则 取最小值时,
取最小值时,  二项展开式中的常数项为 ( )
二项展开式中的常数项为 ( )
A. | B. |
C. | D. |
设变量x,y满足约束条件: .则目标函数z=2x+3y的最小值为( )
.则目标函数z=2x+3y的最小值为( )
| A.6 | B.7 | C.8 | D.23 |
 ,
, 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 (
( ,
, )的最大值为12,则
)的最大值为12,则 的取值范围是( )
的取值范围是( )



 是该目标函数z=ax-y的最优解,则a的取值范围是
是该目标函数z=ax-y的最优解,则a的取值范围是



