题目内容
设m>1,在约束条件 目标函数z=x+my的最大值大于2,则m的取值范围为
目标函数z=x+my的最大值大于2,则m的取值范围为
A. | B. | C.(1,3) | D. |
B
解析试题分析:作出不等式组所表示的平面区域如图所示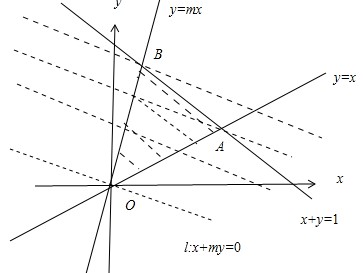
作L:x+my=0,向可行域内平移,越向上,则Z的值越大,从而可得当直线L过B时Z最大
而联立x+y=1,与y=mx可得点B(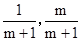 )
)
代入可得Zmax=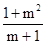 >2
>2
解可得,m>1+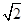 或m<1-
或m<1-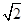
∵m>1∴m>1+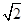 ,故选B.
,故选B.
考点:本题主要考查简单的线性规划,以及利用可行域求最值.
点评:基础题,解题中一定要注意目标函数所对应的直线的斜斜率与边界斜率的大小比较,以确定直线平行的过程中是先过哪个点.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知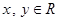 ,且满足
,且满足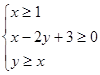 ,则
,则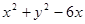 的最小值等于( )
的最小值等于( )
A.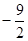 | B.-4 | C.0 | D.-1 |
设变量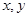 满足
满足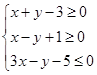 ,设
,设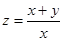 ,则
,则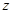 的取值范围是( ).
的取值范围是( ).
A.[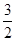 , ,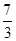 ] ] | B.[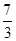 ,3] ,3] | C.[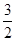 ,3] ,3] | D.[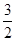 ,+∞) ,+∞) |
设变量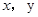 满足
满足 ,则
,则 的最大值为 ( )
的最大值为 ( )
A.  | B. | C. | D. |
若实数 ,则
,则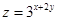 的最大值是( )
的最大值是( )
| A.0 | B.1 | C. | D.9 |
设变量x、y满足 则目标函数z=2x+y的最小值为( )
则目标函数z=2x+y的最小值为( )
A. | B.4 | C.6 | D.以上均不对 |
已知 满足线性约束条件
满足线性约束条件 ,若
,若 ,
,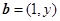 ,则
,则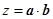 的最大值是( )
的最大值是( )
A.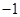 | B.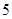 | C.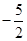 | D. |
设函数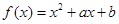 。若
。若 ,则
,则 的最大值为
的最大值为
A. | B.6 | C.7 | D.10 |
目标函数 ,变量
,变量 满足
满足 ,则有 ( )
,则有 ( )
A. | B. 无最大值 无最大值 |
C.  无最小值 无最小值 | D. 既无最大值,也无最小值 既无最大值,也无最小值 |