题目内容
13.已知函数f(x)=xlnx.(1)求f(x)在(e,f(e))处切线方程;
(2)求f(x)最小值;
(3)设F(x)=ax2+f′(x)(a≠0),讨论函数F(x)的单调性.
分析 (1)求出导数,求得切线的斜率和切点,由点斜式方程,即可得到所求切线的方程;
(2)求得函数的定义域,求导函数,确定函数的单调性,即可求得函数f(x)的最小值;
(3)求出函数的导数,并分解因式,讨论a=2,a>2,0<a<2时,导数的符号,进而确定单调性.
解答 解:(1)f(x)=xlnx的导数为f′(x)=1+lnx,
f(x)在点(e,f(e))处的切线斜率为1+1=2,
切点为(e,e),则切线的方程为y-e=2(x-e),
即为2x-y-e=0;
(2)函数的定义域为(0,+∞),
求导函数,可得f′(x)=1+lnx,
令f′(x)=1+lnx=0,可得x=$\frac{1}{e}$,
∴0<x<$\frac{1}{e}$时,f′(x)<0,x>$\frac{1}{e}$时,f′(x)>0,
∴x=$\frac{1}{e}$时,函数取得极小值,也是函数的最小值,
∴f(x)min=f($\frac{1}{e}$)=$\frac{1}{e}$•ln$\frac{1}{e}$=-$\frac{1}{e}$;
(3)F(x)=ax2-(a+2)x+f′(x)=ax2-(a+2)x+1+lnx,
F′(x)=2ax-a-2+$\frac{1}{x}$=$\frac{2a{x}^{2}-(a+2)x+1}{x}$=$\frac{(2x-1)(ax-1)}{x}$,
当a=2时,F′(x)≥0恒成立,函数递增;
当a>2时,$\frac{1}{2}$>$\frac{1}{a}$,由F′(x)>0可得x>$\frac{1}{2}$或0<x<$\frac{1}{a}$,
由F′(x)<0可得$\frac{1}{a}$<x<$\frac{1}{2}$.
可得f(x)在($\frac{1}{a}$,$\frac{1}{2}$)递减,在(0,$\frac{1}{a}$),($\frac{1}{2}$,+∞)递增;
当0<a<2时,$\frac{1}{2}$<$\frac{1}{a}$,由F′(x)>0可得x>$\frac{1}{a}$或0<x<$\frac{1}{2}$,
由F′(x)<0可得$\frac{1}{2}$<x<$\frac{1}{a}$.
可得f(x)在($\frac{1}{2}$,$\frac{1}{a}$)递减,在(0,$\frac{1}{2}$),($\frac{1}{a}$,+∞)递增.
点评 本题考查导数的运用:求切线的方程和单调区间,正确求导和分类讨论是解题的关键,考查运算求解能力,属于中档题.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 |
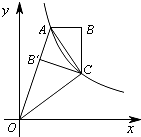 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是2.
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是2.