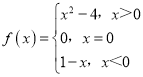ЬтФПФкШн
ЁОЬтФПЁПФГаЃИпвЛФГАрЕФвЛДЮЪ§бЇВтЪдГЩМЈЕФОЅвЖЭМКЭЦЕТЪЗжВМжБЗНЭМвђЪТЙЪЖМЪмЕНВЛЭЌГЬЖШЕФЫ№ЛЕЃЌЕЋПЩМћВПЗжШчЯТЃЌОнДЫНтД№ШчЯТЮЪЬтЃК
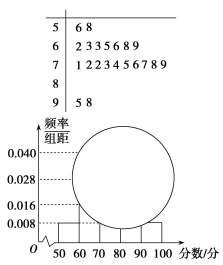
(1)ЧѓЗжЪ§дк[50ЃЌ60)ЕФЦЕТЪМАШЋАрШЫЪ§ЃЛ
(2)ЧѓЗжЪ§дк[80ЃЌ90)ЕФЦЕЪ§ЃЌВЂМЦЫуЦЕТЪЗжВМжБЗНЭМжа[80ЃЌ90)МфЕФОиаЮЕФИпЃЛ
(3)ШєЙцЖЈЃК90Зж(АќКЌ90Зж)вдЩЯЮЊгХауЃЌЯжДгЗжЪ§дк80Зж(АќКЌ80Зж)вдЩЯЕФЪдОэжаШЮШЁСНЗнЗжЮібЇЩњЪЇЗжЧщПіЃЌЧѓдкГщШЁЕФЪдОэжажСЩйгавЛЗнгХауЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ25ШЫЃЛЃЈ2ЃЉ0.016ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМФмЧѓГіЗжЪ§дк[50ЃЌ60ЃЉЕФЦЕТЪЃЌгЩОЅвЖЭМЕУЗжРрдк[50ЃЌ60ЃЉЕФШЫЪ§ЃЌгЩДЫФмЧѓГіШЋАрШЫЪ§ЃЎЃЈ2ЃЉгЩОЅвЖЭМФмЧѓГіЗжЪ§дк[80ЃЌ90ЃЉжЎМфЕФЦЕЪ§ЃЌгЩДЫФмЧѓГіЦЕТЪЗжВМжБЗНЭМжа[80ЃЌ90ЃЉМфЕФОиаЮЕФИпЃЎ(3)РћгУЙХЕфИХаЭЕФИХТЪЙЋЪННтД№.
НтЃК(1)ЗжЪ§дк[50ЃЌ60)ЕФЦЕТЪЮЊ0.008ЁС10ЃН0.08.
гЩОЅвЖЭМжЊЃЌЗжЪ§дк[50ЃЌ60)ЕФЦЕЪ§ЮЊ2ЃЌЫљвдШЋАрШЫЪ§ЮЊ![]() .
.
(2)ЗжЪ§дк[80ЃЌ90)ЕФЦЕЪ§ЮЊ25Ѓ2Ѓ7Ѓ10Ѓ2ЃН4ЃЌ
ЦЕТЪЗжВМжБЗНЭМжа[80ЃЌ90)МфЕФОиаЮЕФИпЮЊ![]() .
.
(3)гЩ(2)ПЩжЊЗжЪ§дк[80ЃЌ100)ЕФШЫЪ§ЮЊ4ЃЋ2ЃН6.
ЩшЗжЪ§дк[80ЃЌ90)ЕФЪдОэЮЊAЃЌBЃЌCЃЌDЃЌЗжЪ§дк[90ЃЌ100]ЕФЪдОэЮЊaЃЌb.
дђДг6ЗнОэжаШЮШЁ2ЗнЃЌЙВга15ИіЛљБОЪТМўЃЌ
ЗжБ№ЪЧABЃЌACЃЌADЃЌAaЃЌAbЃЌBCЃЌBDЃЌBaЃЌBbЃЌCDЃЌCaЃЌCbЃЌDaЃЌDbЃЌabЃЌ
ЦфжажСЩйгавЛЗнгХауЕФЪТМўЙВга9ИіЃЌ
ЗжБ№ЪЧAaЃЌAbЃЌBaЃЌBbЃЌCaЃЌCbЃЌDaЃЌDbЃЌabЃЌ
ЁрдкГщШЁЕФЪдОэжажСЩйгавЛЗнгХауЕФИХТЪЮЊ![]() .
.

 ШЋФмСЗПМОэЯЕСаД№АИ
ШЋФмСЗПМОэЯЕСаД№АИЁОЬтФПЁПРЅУїЪаФГжабЇЕФЛЗБЃЩчЭХВЮееЙњМвЛЗОГБъзМжЦЖЈСЫИУаЃЫљдкЧјгђПеЦјжЪСПжИЪ§гыПеЦјжЪСПЕШМЖЖдгІЙиЯЕШчЯТБэЃЈМйЩшИУЧјгђПеЦјжЪСПжИЪ§ВЛЛсГЌЙ§300ЃЉЃЌИУЩчЭХНЋИУаЃЧјдк2018Фъ100ЬьЕФПеЦјжЪСПжИЪ§МрВтЪ§ОнзїЮЊбљБОЃЌЛцжЦЕФЦЕТЪЗжВМжБЗНЭМШчЭМ4ЃЌАбИУжБЗНЭМЫљЕУЦЕТЪЙРМЦЮЊИХТЪ.
ПеЦјжЪСПжИЪ§ |
|
|
|
|
|
|
ПеЦјжЪСПЕШМЖ | 1МЖгХ | 2МЖСМ | 3МЖЧсЖШЮлШО | 4ЖШжаЖШЮлШО | 5ЖШжиЖШЮлШО | 6МЖбЯжиЮлШО |

ЃЈ1ЃЉЧыЙРЫу2019ФъЃЈвд365ЬьМЦЫуЃЉШЋФъПеЦјжЪСПгХСМЕФЬьЪ§ЃЈЮДТњвЛЬьАДвЛЬьМЦЫуЃЉЃЛ
ЃЈ2ЃЉгУЗжВуГщбљЕФЗНЗЈЙВГщШЁ10ЬьЃЌдђПеЦјжЪСПжИЪ§дк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЬьЪ§жаИїгІГщШЁМИЬь?
ЕФЬьЪ§жаИїгІГщШЁМИЬь?
ЃЈ3ЃЉвбжЊПеЦјжЪСПЕШМЖЮЊ1МЖЪБВЛашвЊОЛЛЏПеЦјЃЌПеЦјжЪСПЕШМЖЮЊ2МЖЪБУПЬьашОЛЛЏПеЦјЕФЗбгУЮЊ2000дЊЃЌПеЦјжЪСПЕШМЖЮЊ3МЖЪБУПЬьашОЛЛЏПеЦјЕФЗбгУЮЊ4000дЊШєдкЃЈ2ЃЉЕФЬѕМўЯТЃЌДгПеЦјжЪСПжИЪ§дк![]() ЕФЬьЪ§жаШЮвтГщШЁСНЬьЃЌЧѓетСНЬьЕФОЛЛЏПеЦјзмЗбгУ
ЕФЬьЪ§жаШЮвтГщШЁСНЬьЃЌЧѓетСНЬьЕФОЛЛЏПеЦјзмЗбгУ![]() ЕФЗжВМСа
ЕФЗжВМСа