题目内容
11.设实数x,y,z满足0<x<y<z<$\frac{π}{2}$,证明:$\frac{π}{2}$+2sinxcosy+2sinycosz>sin2x+sin2y+sin2z.分析 利用作差法,结合三角恒等变换公式,即可证明结论.
解答 证明:由于sin2x+sin2y+sin2z-2sinxcosy-2sinycosz
=$\frac{1}{2}$[(sin2x+sin2y)+(sin2y+sin2z)+(sin2z+sin2x)]-2sinxcosy-2sinycosz
≤sin(x+y)cos(x-y)+sin(y+z)cos(y-z)+sin(z+x)cos(z-x)-2sinxcosycos(x-y)-2sinycoszcos(y-z)
=sin(y-x)cos(x-y)+sin(z-y)cos(y-z)+sin(z+x)cos(z-x)
=$\frac{1}{2}$sin(2y-2x)+$\frac{1}{2}$sin(2z-2y)+sin(z+x)cos(z-x)
=sin(z-x)cos(2y-x-z)+sin(z+x)cos(z-x)
≤sin(z-x)+cos(z-x)≤$\sqrt{2}$<$\frac{π}{2}$
故$\frac{π}{2}$+2sinxcosy+2sinycosz>sin2x+sin2y+sin2z.
点评 本题考查不等式的证明,考查作差法,正确运用三角恒等变换公式是关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
1.甲乙两人独立地对同一目标各射击一次,其命中率分别是0.5和0.6,现已知目标被命中,则它恰是被甲击中的概率为( )
| A. | 0.45 | B. | 0.625 | C. | 0.5 | D. | 0.75 |
16.函数f(x)=$\frac{a}{{log}_{a}x}$(a>1)的图象沿着向量$\overrightarrow{a}$=(-2,1)平移后,若在[2,6]中的最大值与最小值的差为$\frac{2a}{3}$,则a的值为( )
| A. | 16 | B. | $\frac{1}{16}$ | C. | 8 | D. | $\frac{1}{8}$ |
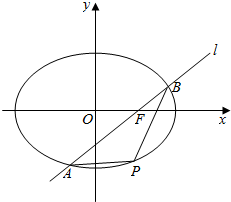 如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F是椭圆C的右焦点,经过点F的直线l与椭圆C相交于A,B两点.
如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F是椭圆C的右焦点,经过点F的直线l与椭圆C相交于A,B两点.