题目内容
19.某汽车销售公司为促销采取了较为灵活的付款方式,对购买一辆10万元的轿车在1年内将款全部付清的前提下,可以选择以下两种分歧付款的方案购车:方案一:分3次付清,购买后4个月第1次付款,再过4个月第2次付款,再过4个月第3次付款:
方案二:分12次付清,购买后一个月第1次付款,再过1个月第2次付款,再过1个月第3次付款…购买12个月后第12次付款.
购买规定分期付款中每期付款额相同,月利率为0.8%,每月利息按复利计算,试比较以上两种方案的那一种方案付款总额较少?
分析 分别计算两种方案的付款总额,进行比较即可.
解答 解:(1)对于方案一,设每次付款额为x1万元,那么一年后,第一次付款的本金为1.0088x1万元,第二次付款的本金为1.0084x1万元,第3次付款的本金为x1万元,则1.0088x1+1.0084x1+x1=10(1+0.8%)12.
解得x1≈3.552(万元).
付款总额为3×3.552=10.656(万元).
对于方案二,设每次付款为x2万元,那么一年后,第一次付款的本金为1.00811x2万元,第2次付款的本金为1.00810x2万元,…,第12次付款的本金为x2万元.则1.00811x2+1.00810x2+…+1.008x2+x2=10×1.00812.
解得x2≈0.88(万元).
付款总额为12×0.88=10.56(万元),
∵10.658>10.56,
∴第二种方案付款总额较少.
点评 本题主要考查函数的应用问题,根据条件建立方程关系是解决本题的关键.

练习册系列答案
相关题目
9.若直线a∥α,直线b∥α,则a与b( )
| A. | 平行 | B. | 异面 | C. | 平行或异面 | D. | 相交、平行或异面 |

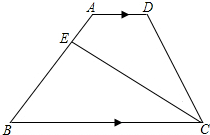 如图所示,在梯形ABCD中,BC∥AD,BC=3AD,点E在AB边上,且$\frac{AE}{BE}$=$\frac{1}{4}$,求△BEC的面积与四边形AECD的面积之比.
如图所示,在梯形ABCD中,BC∥AD,BC=3AD,点E在AB边上,且$\frac{AE}{BE}$=$\frac{1}{4}$,求△BEC的面积与四边形AECD的面积之比.