题目内容
(本题满分14分)
对数列{an},规定{△an}为数列{an}的一阶差分数列,其中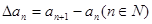 。
。
对自然数k,规定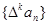 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中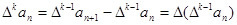 。
。
(1)已知数列{an}的通项公式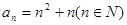 ,试判断
,试判断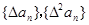 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列{an}首项a1=1,且满足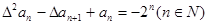 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
(3)对(2)中数列{an},是否存在等差数列{bn},使得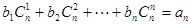 对一切自然
对一切自然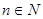 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
对数列{an},规定{△an}为数列{an}的一阶差分数列,其中
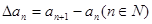 。
。对自然数k,规定
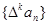 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中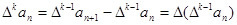 。
。(1)已知数列{an}的通项公式
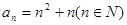 ,试判断
,试判断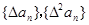 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?(2)若数列{an}首项a1=1,且满足
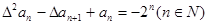 ,求数列{an}的通项公式。
,求数列{an}的通项公式。(3)对(2)中数列{an},是否存在等差数列{bn},使得
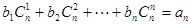 对一切自然
对一切自然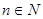 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。(1)根据给定的新定义来分析得到结论。
(2)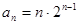
(3)存在等差数列 ,bn=n,使得
,bn=n,使得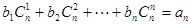 对一切自然
对一切自然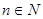 都成立。
都成立。
(2)
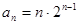
(3)存在等差数列
 ,bn=n,使得
,bn=n,使得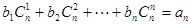 对一切自然
对一切自然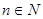 都成立。
都成立。试题分析:解:(1)
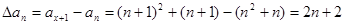
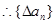 是首项为4,公差为2的等差数列
是首项为4,公差为2的等差数列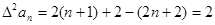
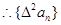 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列(2)
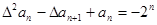 ,即
,即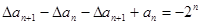 ,即
,即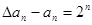
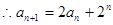
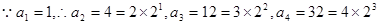
猜想:
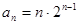
证明:i)当n=1时,
 ;
;ii)假设n=k时,
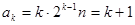 时,
时,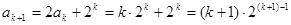 结论也成立
结论也成立∴由i)、ii)可知,
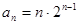
(3)
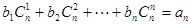 ,即
,即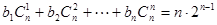
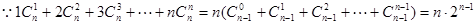
∴存在等差数列
 ,bn=n,使得
,bn=n,使得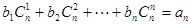 对一切自然
对一切自然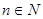 都成立。
都成立。点评:解决该试题的关键是利用数列的定义以及等差数列的概念结合得到结论,属于基础题。

练习册系列答案
相关题目
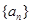 满足,
满足,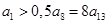 ,则前n项和
,则前n项和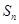 取最大值时,n的值为
取最大值时,n的值为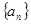 的前项
的前项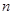 和为
和为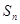 ,若
,若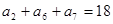 ,则
,则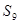 的值为( )
的值为( )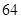
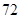
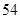
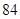
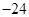 的等差数列,从第10项开始为正数,则公差
的等差数列,从第10项开始为正数,则公差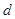 的取值范围是( )
的取值范围是( )
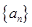 满足:
满足: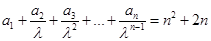 (其中常数
(其中常数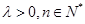 ).
).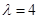 时,数列
时,数列 为数列
为数列 项和.求证:若任意
项和.求证:若任意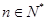 ,
,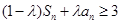
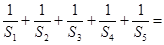
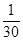
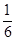
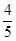
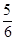
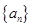 的前
的前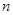 项和为
项和为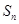 ,且满足
,且满足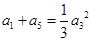 ,
,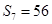 .
.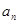 ;
;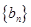 满足
满足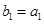 且
且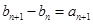 ,求数列
,求数列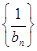 的前
的前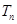 .
.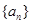 满足:
满足: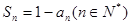 ,其中
,其中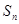 为
为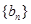 满足
满足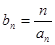 ,求
,求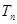 .
.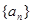 满足
满足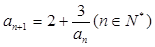 ,数列
,数列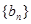 满足
满足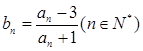 ,
,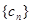 满足
满足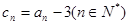 .
.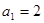 ,证明数列
,证明数列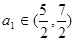 ,证明数列
,证明数列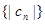 的前
的前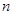 项和
项和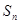 满足
满足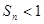 。
。