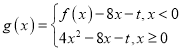题目内容
【题目】已知函数![]() (
(![]() ,
,![]() )
)
(1)若![]() ,求函数
,求函数![]() 的单调区间与极值;
的单调区间与极值;
(2)若在区间![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)求出![]() 的表达式,定义域以及导数,然后判断导函数的符号,求出单调区间.
的表达式,定义域以及导数,然后判断导函数的符号,求出单调区间.
(2)若在区间![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立,其充要条件是
成立,其充要条件是![]() 在区间
在区间![]() 上的最小值小于0即可.利用导数研究函数在闭区
上的最小值小于0即可.利用导数研究函数在闭区![]() 上的最小值,先求出
上的最小值,先求出![]() 导函数f,然后讨论研究函数在
导函数f,然后讨论研究函数在![]() 上的单调性,将
上的单调性,将![]() 的各极值与其端点的函数值比较,其中最小的一个就是最小值.
的各极值与其端点的函数值比较,其中最小的一个就是最小值.
试题解析:(1)当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,又函数
,又函数![]() 的定义域为
的定义域为![]() ,由
,由 ![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
![]() 时,
时,![]() 有极小值
有极小值![]() ,无极大值
,无极大值
(2)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,即
成立,即![]() 在区间
在区间![]() 上单调递减
上单调递减
故![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,
,![]()
当![]() 即
即![]() 时,
时,
①若![]() ,则
,则![]() 对
对![]() 成立,所以
成立,所以![]() 在区间
在区间![]() 上单调递减
上单调递减
则![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
显然,![]() 在区间
在区间![]() 的最小值小于
的最小值小于![]() 不成立.
不成立.
②若![]() ,即
,即![]() 时,则有
时,则有![]() 在
在![]() 单减,
单减,![]() 单增,
单增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,由
,由![]()
![]() ,
,
得![]() ,解得
,解得![]() ,即
,即![]() ,综上,
,综上,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某服装批发市场1-5月份的服装销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销售量 | 3 | 6 | 4 | 7 | 8 |
利润 | 19 | 34 | 26 | 41 | 46 |
(1)从这五个月的利润中任选2个,分别记为![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知销售量![]() 与利润
与利润![]() 大致满足线性相关关系,请根据前4个月的数据,求出
大致满足线性相关关系,请根据前4个月的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元,则认为得到的利润的估计数据是理想的.请用表格中第5个月的数据检验由(2)中回归方程所得的第5个月的利润的估计数据是否理想.参考公式:  .
.
【题目】以“你我中国梦,全民建小康”为主题“社会主义核心价值观”为主线,为了解![]() 、
、![]() 两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对
两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对![]() 、
、![]() 地区的
地区的![]() 名观众进行统计,统计结果如下:
名观众进行统计,统计结果如下:
非常满意 | 满意 | 合计 | |
|
|
| |
|
|
| |
合计 |
在被调查的全体观众中随机抽取![]() 名“非常满意”的人是
名“非常满意”的人是![]() 地区的概率为
地区的概率为![]() ,且
,且![]() .
.
(1)现从![]() 名观众中用分层抽样的方法抽取
名观众中用分层抽样的方法抽取![]() 名进行问卷调查,则应抽取“满意”的
名进行问卷调查,则应抽取“满意”的![]() 、
、![]() 地区的人数各是多少?
地区的人数各是多少?
(2)在(1)抽取的“满意”的观众中,随机选出![]() 人进行座谈,求至少有两名是
人进行座谈,求至少有两名是![]() 地区观众的概率?
地区观众的概率?
(3)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系?
的把握认为观众的满意程度与所在地区有关系?
附:
|
|
|
|
|
|
|
|
,![]()
【题目】某校参加夏令营的同学有3名男同学![]() 和3名女同学
和3名女同学![]() ,其所属年级情况如下表:
,其所属年级情况如下表:
高一年级 | 高二年级 | 高三三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母写出这个试验的样本空间;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件![]() 的样本点,并求事件
的样本点,并求事件![]() 发生的概率.
发生的概率.