题目内容
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同零点,是否存在实数
的两个不同零点,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数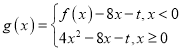 ,存在
,存在![]() 个零点.
个零点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设![]() 分别是这
分别是这![]() 个零点中的最小值与最大值,求
个零点中的最小值与最大值,求![]() 的最大值.
的最大值.
【答案】(1) 不存在.理由见解析;
(2) (i) ![]() (ii)
(ii) ![]()
【解析】
(1) .假设存在实数![]() 满足题意,由韦达定理可得:
满足题意,由韦达定理可得:![]()
![]() ,解得
,解得![]() ,又
,又![]() ,即
,即![]() ,综合可得假设不成立;
,综合可得假设不成立;
(2) (i)作出函数![]() 的图象,观察图像即可求出
的图象,观察图像即可求出![]() 的取值范围;
的取值范围;
(ii)设直线![]() 与此图象的最左边和最右边的交点分别为
与此图象的最左边和最右边的交点分别为![]() .即
.即![]() ,因为
,因为![]()
![]() ,代入运算可得解.
,代入运算可得解.
解:(1)依题意可知,![]() .假设存在实数
.假设存在实数![]() ,使
,使![]() 成立.
成立.
因为![]() 有两个不同零点,.
有两个不同零点,.
所以![]() ,解得
,解得![]() .
.
由韦达定理得![]()
所以![]()
![]()
解得![]() ,而
,而![]() ,故不存在.
,故不存在.
(2)因为![]() ,设
,设![]() ,则
,则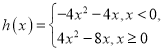 ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
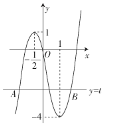
(i)作出函数![]() 的图象,如图所示,所以
的图象,如图所示,所以![]() .
.
(ii)设直线![]() 与此图象的最左边和最右边的交点分别为
与此图象的最左边和最右边的交点分别为![]() .
.
由![]() ,得
,得![]()
由![]() ,得
,得![]()
所以![]()
因为![]()
![]() ,
,
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
故![]() 的最大值为
的最大值为![]() .
.

【题目】从![]() 年
年![]() 月份,某市街头出现共享单车,到
月份,某市街头出现共享单车,到![]() 月份,根据统计,市区所有人骑行过共享单车的人数已占
月份,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是大学生(含大中专及高职),该市区人口按
是大学生(含大中专及高职),该市区人口按![]() 万计算,大学生人数约
万计算,大学生人数约![]() 万人.
万人.
(1)任选出一名大学生,求他(她)骑行过共享单车的概率;
(2)随单车投放数量增加,乱停乱放成为城市管理的问题,以下是累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间的关系图表:
之间的关系图表:
累计投放单车数量 |
|
|
|
|
|
乱停乱放单车数量 |
|
|
|
|
|
①计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
②已知该市共有五个区,其中有两个区的单车乱停乱放数量超过标准.在“双创”活动中,检查组随机抽取三个区调查单车乱停乱放数量, ![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘法估计公式分别为
中的斜率和截距的最小二乘法估计公式分别为
![]() .
.
【题目】进入12月以业,在华北地区连续出现两次重污染天气的严峻形势下,我省坚持保民生,保蓝天,各地严格落实机动车限行等一系列“管控令”,某市交通管理部门为了了解市民对“单双号限行”的态度,随机采访了200名市民,将他们的意见和是否拥有私家车的情况进行了统计,得到如下的![]() 列联表:
列联表:
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断能否在犯错误的概率不超过![]() 的前提下认为“对限行的态度与是否拥有私家车有关”;
的前提下认为“对限行的态度与是否拥有私家车有关”;
(2)为了了解限行之后是否对交通拥堵、环境染污起到改善作用,从上述调查的不赞同限行的人员中按是否拥有私家车分层抽样抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少有1人没有私家车的概率.
附: 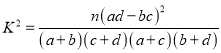 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
