题目内容
已知函数f(x)=ln(1+x2)+ax(a≤0).
(1)若f(x)在x=0处取得极值,求a的值;
(2)讨论f(x)的单调性;
(3)证明:(1+
)(1+
)…(1+
)<e1-
(n∈N*,e为自然对数的底数)
(1)若f(x)在x=0处取得极值,求a的值;
(2)讨论f(x)的单调性;
(3)证明:(1+
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 4n |
| 1 |
| 2n |
(1)f′(x)=
+a,
∵x=0是f(x)的一个极值点,∴f′(0)=0,
∴a=0
∵x<0,f′(x)<0;x>0,f′(x)>0
∴a=0符合条件…(3分)
(2)f′(x)=
+a=
.…(4分)
①若a=0时,由(1)知,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;…(5分)
②若
,即当a≤-1时,f'(x)≤0对x∈R恒成立.
∴f(x)在(-∞,+∞)上单调递减.…(6分)
③若当-1<a<0时,由f'(x)>0得ax2+2x+a>0,∴
<x<
.
再令f'(x)<0可得x>
或x<
.
∴f(x)在(
,
)上单调递增,在(-∞,
),(
,+∞)上单调递减.…(9分)
(3)证明:由(2)知,当a=-1时,f(x)在(-∞,+∞)上单调递减;
当x∈(0,+∞)时,由f(x)=ln(1+x2)-x<f(0)=0,∴ln(1+x2)<x
∴ln[(1+
)(1+
)…(1+
)]=ln(1+
)+ln(1+
)+…+ln(1+
)<
+
+…+
=
=1-
∴(1+
)(1+
)…(1+
)<e1-
.…(14分)
| 2x |
| 1+x2 |
∵x=0是f(x)的一个极值点,∴f′(0)=0,
∴a=0
∵x<0,f′(x)<0;x>0,f′(x)>0
∴a=0符合条件…(3分)
(2)f′(x)=
| 2x |
| 1+x2 |
| ax2+2x+a |
| 1+x2 |
①若a=0时,由(1)知,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;…(5分)
②若
|
∴f(x)在(-∞,+∞)上单调递减.…(6分)
③若当-1<a<0时,由f'(x)>0得ax2+2x+a>0,∴
-1+
| ||
| a |
-1-
| ||
| a |
再令f'(x)<0可得x>
-1-
| ||
| a |
-1+
| ||
| a |
∴f(x)在(
-1+
| ||
| a |
-1-
| ||
| a |
-1+
| ||
| a |
-1-
| ||
| a |
(3)证明:由(2)知,当a=-1时,f(x)在(-∞,+∞)上单调递减;
当x∈(0,+∞)时,由f(x)=ln(1+x2)-x<f(0)=0,∴ln(1+x2)<x
∴ln[(1+
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 4n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| ||||
1-
|
| 1 |
| 2n |
∴(1+
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 4n |
| 1 |
| 2n |

练习册系列答案
相关题目
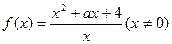 。
。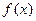 为奇函数,求
为奇函数,求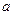 的值;
的值;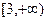 上恒大于0,求
上恒大于0,求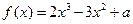 的极大值为
的极大值为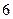 ,则
,则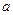 等于( )
等于( )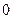
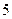
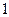
 时对应的点不一定是极值点
时对应的点不一定是极值点 取得极大值或极小值时的
取得极大值或极小值时的 的值分别为
的值分别为 和
和 ,则( )
,则( )


