题目内容
12.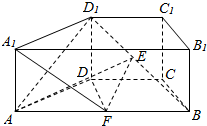 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2DC=2,E为BD1的中点,F为AB的中点,∠DAB=60°.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2DC=2,E为BD1的中点,F为AB的中点,∠DAB=60°.(Ⅰ)求证:EF∥平面ADD1A1;
(Ⅱ)若BB1=$\frac{{\sqrt{2}}}{2}$,求A1F与平面DEF所成角的正弦值.
分析 (Ⅰ)根据条件容易得出EF∥AD1,根据线面平行的判定定理即可得出EF∥平面ADD1A1;
(Ⅱ)取AF中点G,连接DG,可以说明DG,DC,DD1三直线两两垂直,从而分别以这三直线为x,y,z轴,建立空间直角坐标系,求出空间一些点的坐标,从而可以得出向量$\overrightarrow{DE},\overrightarrow{DF},\overrightarrow{{A}_{1}F}$的坐标,可设平面DEF的法向量为$\overrightarrow{m}=(x,y,z)$,根据$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DE}=0}\\{\overrightarrow{m}•\overrightarrow{DF}=0}\end{array}\right.$可以求出法向量$\overrightarrow{m}$,可设A1F和平面DEF所成角为θ,从而根据sin$θ=|cos<\overrightarrow{m},\overrightarrow{{A}_{1}F}>|$即可求出sinθ.
解答 解:(Ⅰ)证明:E为BD1的中点,F为AB的中点;
∴EF为△ABD1的中位线;
∴EF∥AD1,AD1?平面ADD1A1,EF?平面ADD1A1;
∴EF∥平面ADD1A1;
(Ⅱ)AB∥CD,AB=2DC,F为AB中点;
∴DC∥FB,且DC=FB;
∴四边形DCBF为平行四边形;
∴DF=CB,底面ABCD是等腰梯形,∠DAB=60°;
∴△ADF为等边三角形,∠ADF=60°;
取AF中点G,连接DG,则∠GDC=90°;
即DG⊥DC,又DD1⊥底面ABCD;
∴DG,DC,DD1三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则: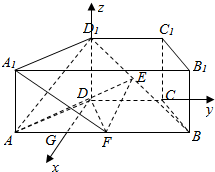 $D(0,0,0),{D}_{1}(0,0,\frac{\sqrt{2}}{2}),B(\frac{\sqrt{3}}{2},\frac{3}{2},0)$,$E(\frac{\sqrt{3}}{4},\frac{3}{4},\frac{\sqrt{2}}{4}),F(\frac{\sqrt{3}}{2},\frac{1}{2},0),{A}_{1}(\frac{\sqrt{3}}{2},-\frac{1}{2},\frac{\sqrt{2}}{2})$;
$D(0,0,0),{D}_{1}(0,0,\frac{\sqrt{2}}{2}),B(\frac{\sqrt{3}}{2},\frac{3}{2},0)$,$E(\frac{\sqrt{3}}{4},\frac{3}{4},\frac{\sqrt{2}}{4}),F(\frac{\sqrt{3}}{2},\frac{1}{2},0),{A}_{1}(\frac{\sqrt{3}}{2},-\frac{1}{2},\frac{\sqrt{2}}{2})$;
∴$\overrightarrow{DE}=(\frac{\sqrt{3}}{4},\frac{3}{4},\frac{\sqrt{2}}{4}),\overrightarrow{DF}=(\frac{\sqrt{3}}{2},\frac{1}{2},0)$,$\overrightarrow{{A}_{1}F}=(0,1,-\frac{\sqrt{2}}{2})$;
设平面DEF的法向量为$\overrightarrow{m}=(x,y,z)$,则:$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DE}=\frac{\sqrt{3}}{4}x+\frac{3}{4}y+\frac{\sqrt{2}}{4}z=0}\\{\overrightarrow{m}•\overrightarrow{DF}=\frac{\sqrt{3}}{2}x+\frac{1}{2}y=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{y=-\frac{\sqrt{2}}{2}z}\\{x=\frac{\sqrt{6}}{6}z}\end{array}\right.$,取z=1,则$\overrightarrow{m}=(\frac{\sqrt{6}}{6},-\frac{\sqrt{2}}{2},1)$;
设A1F和平面DEF所成角为θ,则sinθ=$|cos<\overrightarrow{{A}_{1}F},\overrightarrow{m}>|=\frac{\sqrt{2}}{\sqrt{1+\frac{1}{2}}•\sqrt{\frac{1}{6}+\frac{1}{2}+1}}$=$\frac{2\sqrt{5}}{5}$;
∴A1F和平面DEF所成角的正弦值为$\frac{2\sqrt{5}}{5}$.
点评 考查线面平行的判定定理,直四棱柱的定义,平行四边形的定义,线面垂直的性质,以及通过建立空间直角坐标系,利用空间向量解决线面角问题的方法,平面法向量的概念,向量夹角余弦的坐标公式,能求空间点的坐标,清楚直线和平面所成角与直线的方向向量和平面法向量的夹角的关系.

 阅读快车系列答案
阅读快车系列答案| A. | ${log}_{\frac{1}{2}}$t<1<t | B. | t<1<${log}_{\frac{1}{2}}$t | C. | ${log}_{\frac{1}{2}}$t<t<1 | D. | t<${log}_{\frac{1}{2}}$t<1 |
| A. | 7 | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
| A. | a<-2 | B. | a>-2 | C. | a≤-4 | D. | a<-4 |