��Ŀ����
7����֪����$\overrightarrow{m}$=��sinx��-1����$\overrightarrow{n}$=��cosx��$\frac{3}{2}$����f��x��=��$\overrightarrow{m}$+$\overrightarrow{n}$��•$\overrightarrow{m}$����1����f��x������С�����ڼ������������䣻
��2����x��[0��$\frac{��}{2}$]ʱ����f��x����ֵ��
��3����f��x����ͼ������$\frac{3��}{8}$����λ���g��x����ͼ����g��x����[-$\frac{��}{3}$��$\frac{��}{3}$]�ϵ����ֵ��
���� ��1�������������������ʡ��Ͳʽ�뱶�ǹ�ʽ�ɵã�f��x��=��sinx+cosx��•sinx-$\frac{1}{2}$=$\frac{\sqrt{2}}{2}$$sin��2x-\frac{��}{4}��$���ɵ�$T=\frac{2��}{2}$����$-\frac{��}{2}+2k��$��$2x-\frac{��}{4}$��$2k��+\frac{��}{2}$��������ɵó��������䣮
��2����x��[0��$\frac{��}{2}$]ʱ���ɵ�$-\frac{��}{4}��2x-\frac{��}{4}$��$\frac{3��}{4}$���ɵ�$sin��2x-\frac{��}{4}��$��$[-\frac{\sqrt{2}}{2}��1]$�����ɵó�f��x����ֵ��
��3����f��x����ͼ������$\frac{3��}{8}$����λ���g��x����ͼ�ɵ�g��x��=$\frac{\sqrt{2}}{2}$cos2x������x��[-$\frac{��}{3}$��$\frac{��}{3}$]���ɵ�cos2x��$[-\frac{1}{2}��1]$�����ɵó���
��� �⣺��1��f��x��=��$\overrightarrow{m}$+$\overrightarrow{n}$��•$\overrightarrow{m}$=��sinx+cosx��•sinx-$\frac{1}{2}$
=sin2x+sinxcosx-$\frac{1}{2}$
=$\frac{1-cos2x}{2}$+$\frac{1}{2}$sin2x-$\frac{1}{2}$
=$\frac{\sqrt{2}}{2}$$sin��2x-\frac{��}{4}��$��
��$T=\frac{2��}{2}$=��
��$-\frac{��}{2}+2k��$��$2x-\frac{��}{4}$��$2k��+\frac{��}{2}$�����$k��-\frac{��}{8}$��x��$\frac{3��}{8}+k��$��k��Z��
�ຯ��f��x���ĵ�����������Ϊ[$k��-\frac{��}{8}$��$\frac{3��}{8}+k��$]��k��Z��
��2����x��[0��$\frac{��}{2}$]ʱ��
$-\frac{��}{4}��2x-\frac{��}{4}$��$\frac{3��}{4}$��
��$sin��2x-\frac{��}{4}��$��$[-\frac{\sqrt{2}}{2}��1]$��
��f��x����ֵ��Ϊ$[-\frac{1}{2}��\frac{\sqrt{2}}{2}]$��
��3����f��x����ͼ������$\frac{3��}{8}$����λ���g��x����ͼ��
��g��x��=$\frac{\sqrt{2}}{2}$$sin[2��x+\frac{3��}{8}��-\frac{��}{4}]$=$\frac{\sqrt{2}}{2}$cos2x��
��x��[-$\frac{��}{3}$��$\frac{��}{3}$]��
��cos2x��$[-\frac{1}{2}��1]$��
��$\frac{\sqrt{2}}{2}$cos2x��$[-\frac{\sqrt{2}}{4}��\frac{\sqrt{2}}{2}]$��
�ຯ��g��x�������ֵΪ��$\frac{\sqrt{2}}{2}$��
���� ���⿼���������������������ʡ��Ͳʽ�����ǹ�ʽ�����Ǻ�����ͼ�������ʣ�������������������������������е��⣮

 â���̸����������������ϵ�д�
â���̸����������������ϵ�д�| A�� | ��-�ޣ�0�� | B�� | ��0��+�ޣ� | C�� | ��-�ޣ�0���ȣ�0��+�ޣ� | D�� | R |
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
| A�� | 1 | B�� | 2 | C�� | -1 | D�� | $\frac{1}{2}$ |
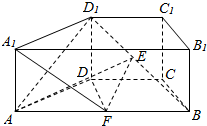 ��ͼ��ֱ������ABCD-A1B1C1D1�У�����ABCD�ǵ������Σ�AB��CD��AB=2DC=2��EΪBD1���е㣬FΪAB���е㣬��DAB=60�㣮
��ͼ��ֱ������ABCD-A1B1C1D1�У�����ABCD�ǵ������Σ�AB��CD��AB=2DC=2��EΪBD1���е㣬FΪAB���е㣬��DAB=60�㣮