题目内容
20.已知a,b为异面直线,A,B∈a,C,D∈b,a∥α,b∥α,AC∩α=E,BD∩α=G,BC∩α=H,求证:EG与FH相互平分.分析 要证明EG与FH相互平分,只要证明EFGH是平行四边形即可,利用线面平行的性质进行证明即可.
解答 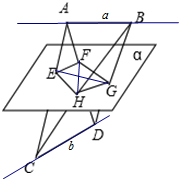 解:∵AC∩AD=A,
解:∵AC∩AD=A,
∴AC与AD确定平面ACD,
∵C,D∈b,b∥α,
∴CD∥α,面ACD∩α=EF,
∴EF∥CD,
∵BC∩BD=B,
∴BC与BD确定平面BCD,
∵CD∥α,面BCD∩α=GH,
∴GH∥CD,
∴EF∥GH.
∵AC∩BC=C,
∴AC与BC确定平面ACB,
∵AB∥α,面ACB∩α=EH,
∴EH∥AB,
∵BD∩AD=D,
∴BD与AD确定平面ABD,
∵AB∥α,面ABD∩α=GF,
∴GF∥AB,
∴EH∥GF.
∴四边形EFGH是平行四边形.
即EG与FH相互平分.
点评 本题考查了直线和平面平行的判定和性质,考查了学生的空间想象能力和思维能力,利用线面平行的判定定理和性质定理是解决本题的关键.

练习册系列答案
相关题目
 已知函数$f(x)=Asin(ωx+\frac{π}{6})$(A>0,ω>0)的部分图象如图所示,其中M$(-\frac{1}{6},0)$为图象与x轴的交点,$P(\frac{1}{3},2)$为图象的最高点.
已知函数$f(x)=Asin(ωx+\frac{π}{6})$(A>0,ω>0)的部分图象如图所示,其中M$(-\frac{1}{6},0)$为图象与x轴的交点,$P(\frac{1}{3},2)$为图象的最高点.