题目内容
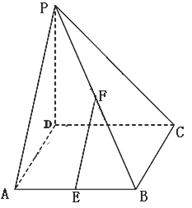
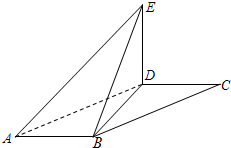
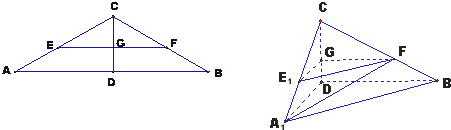
如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=______.


由题意可知,∠FAD=∠EBC=60°,连接EC,
在三角形EBC中,由余弦定理可得EC=
又AB=CB=2a,BE=a
所以EC=
=
a
又矩形ABEF和正方形ABCD可得AB⊥面EBC,即CD⊥面EBC
所以∠ECD为直角
在Rt△ECD中,由勾股定理得ED=
=
=
a
故答案为
a
在三角形EBC中,由余弦定理可得EC=
| EB2+BC2-2×EB×BC×cos60° |
又AB=CB=2a,BE=a
所以EC=
| a2+4a2-2×a×2a×cos60° |
| 3 |
又矩形ABEF和正方形ABCD可得AB⊥面EBC,即CD⊥面EBC
所以∠ECD为直角
在Rt△ECD中,由勾股定理得ED=
| EC2+CD2 |
| 3a2+4a2 |
| 7 |
故答案为
| 7 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
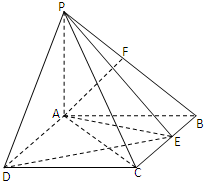
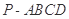 中,
中,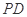 ⊥底面
⊥底面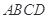 ,底面
,底面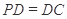 ,
,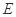 ,
,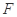 分别是
分别是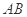 ,
,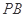 的 中点.
的 中点.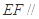 平面
平面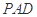 ;
;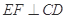 ;
;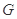 是线段
是线段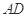 上一动点,试确定
上一动点,试确定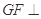 平面
平面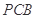 ,并证明你的结论.
,并证明你的结论.