题目内容
(本题满分14分)已知函数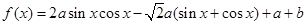 的定义域为
的定义域为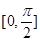 ,值域为
,值域为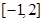 .
.
(1)求实数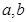 的值;
的值;
(2)数列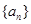 中,有
中,有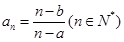 . 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
. 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
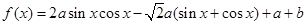 的定义域为
的定义域为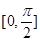 ,值域为
,值域为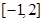 .
.(1)求实数
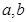 的值;
的值;(2)数列
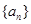 中,有
中,有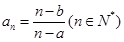 . 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
. 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.(1)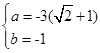 ; (2)当n=1时,最小项为
; (2)当n=1时,最小项为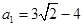 ,无最大项;
,无最大项;
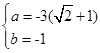 ; (2)当n=1时,最小项为
; (2)当n=1时,最小项为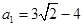 ,无最大项;
,无最大项;本试题主要是考查了三角函数与数列的综合运用。
(1)设 ,
,
由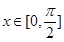 ,知
,知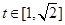 ,又
,又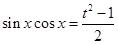 ,
,
则函数为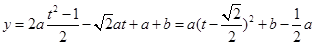 根据单调性分析得到参数a,b的值。
根据单调性分析得到参数a,b的值。
(2)在第一问的基础上,进一步运用定义法得到数列的单调性,进而得到最小项的值。
解:(1)设 ,
,
由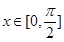 ,知
,知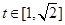 , ………………2分
, ………………2分
又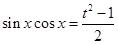 ,
,
则函数为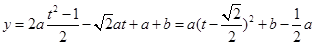 ,…………………4分
,…………………4分
即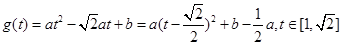 , …………5分
, …………5分
①当a>0时,g(t)在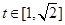 单调递增,
单调递增,
有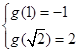 ,得
,得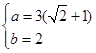 ; …………………6分
; …………………6分
①当a=0时,g(t)=b不合; …………………7分
②当a<0时,g(t)在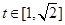 单调递减,
单调递减,
有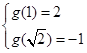 ,得
,得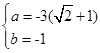 ; …………………8分
; …………………8分
(2)①当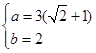 ,则
,则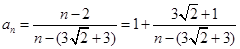 ,
,
由图象知,当n=7时,最小项为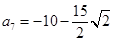 ,
,
当n=8时,最大项为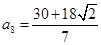 ; …………………11分
; …………………11分
②当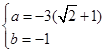 ,则
,则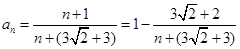 ,
,
由图象知,当n=1时,最小项为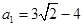 ,无最大项;……………14分
,无最大项;……………14分
(1)设
 ,
,由
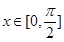 ,知
,知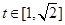 ,又
,又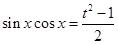 ,
,则函数为
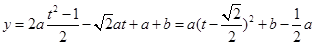 根据单调性分析得到参数a,b的值。
根据单调性分析得到参数a,b的值。(2)在第一问的基础上,进一步运用定义法得到数列的单调性,进而得到最小项的值。
解:(1)设
 ,
,由
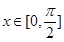 ,知
,知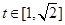 , ………………2分
, ………………2分又
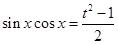 ,
,则函数为
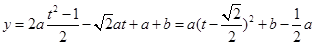 ,…………………4分
,…………………4分即
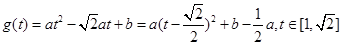 , …………5分
, …………5分①当a>0时,g(t)在
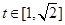 单调递增,
单调递增,有
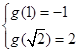 ,得
,得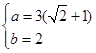 ; …………………6分
; …………………6分①当a=0时,g(t)=b不合; …………………7分
②当a<0时,g(t)在
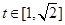 单调递减,
单调递减,有
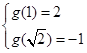 ,得
,得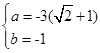 ; …………………8分
; …………………8分(2)①当
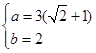 ,则
,则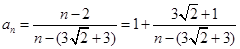 ,
,由图象知,当n=7时,最小项为
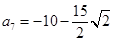 ,
,当n=8时,最大项为
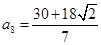 ; …………………11分
; …………………11分②当
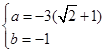 ,则
,则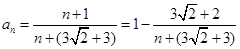 ,
,由图象知,当n=1时,最小项为
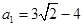 ,无最大项;……………14分
,无最大项;……………14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )的部分图象.
)的部分图象. =
= ,0<α<
,0<α< ,求cosα的值.
,求cosα的值.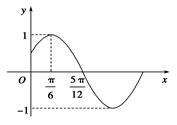
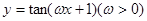 的最小正周期为
的最小正周期为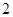 ,则
,则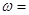 .
.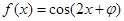 的图象关于点
的图象关于点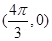 成中心对称,且
成中心对称,且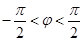 ,则函数
,则函数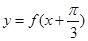 为
为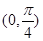 上单调递增
上单调递增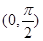 上单调递增
上单调递增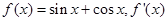 是
是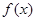 的导函数.
的导函数.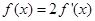 ,求
,求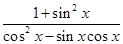 的值.
的值. 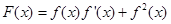 (
(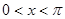 )的单调增区间。
)的单调增区间。 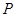 是函数
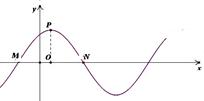
是函数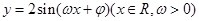 图象的最高点,
图象的最高点,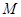 、
、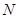 是图象与
是图象与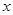 轴的交点,若
轴的交点,若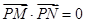 ,则
,则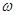 = .
= .
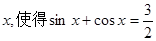 ;
;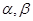 为第一象限角,且
为第一象限角,且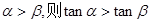 ;
;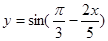 是最小正周期为
是最小正周期为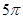 ;
;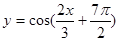 是奇函数;
是奇函数;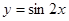 的图像向左平移
的图像向左平移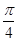 个单位,得到
个单位,得到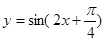 的图像。
的图像。 的最大值是3,则它的最小值_____________
的最大值是3,则它的最小值_____________ 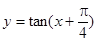 的定义域是
的定义域是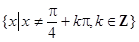 ;
;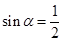 ,且
,且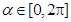 ,则
,则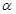 的取值集合是
的取值集合是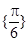 ;
;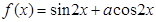 的图象关于直线
的图象关于直线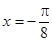 对称,则
对称,则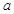 的值等于
的值等于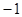 ;
;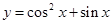 的最小值为
的最小值为