题目内容
(本小题满分12分)
右图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象.
)的部分图象.
(1)求函数f(x)的解析式;
(2)若f =
= ,0<α<
,0<α< ,求cosα的值.
,求cosα的值.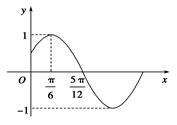
右图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 )的部分图象.
)的部分图象.(1)求函数f(x)的解析式;
(2)若f
 =
= ,0<α<
,0<α< ,求cosα的值.
,求cosα的值.
(1) f(x)=sin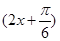 .
.
(2) cosα=[(α+ )-
)- ]=cos
]=cos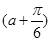 cos
cos +sin
+sin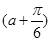 sin
sin =
=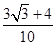 .
.
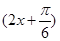 .
.(2) cosα=[(α+
 )-
)- ]=cos
]=cos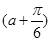 cos
cos +sin
+sin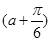 sin
sin =
=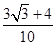 .
.(I)观察图象可得函数的最值为1,且函数先出现最大值可得A=1;函数的周期T=π,结合周期公式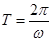 可求ω;由函数的图象过
可求ω;由函数的图象过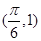 代入可得φ.
代入可得φ.
(II)由(I)可得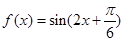 ,从而由
,从而由 ,代入整理可得
,代入整理可得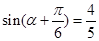
,结合已知 ,可得利用
,可得利用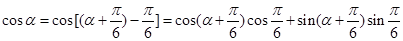 代入求值即可.
代入求值即可.
(1)由图象知A=1 .………………1分
f(x)的最小正周期T=4×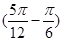 =π,故ω=
=π,故ω=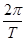 =2.……3分
=2.……3分
将点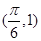 代入f(x)的解析式得sin
代入f(x)的解析式得sin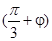 =1,
=1,
∴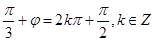 ,即
,即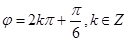 ,
,
又|φ|< ,∴φ=
,∴φ= .………………………………5分
.………………………………5分
故函数f(x)的解析式为f(x)=sin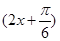 .…………………6分
.…………………6分
(2)由f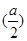 =
= ,得sin
,得sin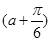 =
= ,由0<α<
,由0<α< ,得
,得 <α+
<α+ <
< ,
,
∴cos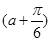 =
=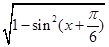 =
=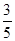 .………………………9分
.………………………9分
∴cosα=[(α+ )-
)- ]=cos
]=cos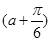 cos
cos +sin
+sin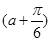 sin
sin =
=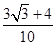 .………12分
.………12分
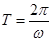 可求ω;由函数的图象过
可求ω;由函数的图象过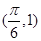 代入可得φ.
代入可得φ.(II)由(I)可得
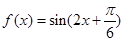 ,从而由
,从而由 ,代入整理可得
,代入整理可得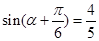
,结合已知
 ,可得利用
,可得利用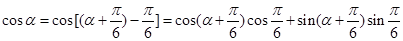 代入求值即可.
代入求值即可.(1)由图象知A=1 .………………1分
f(x)的最小正周期T=4×
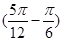 =π,故ω=
=π,故ω=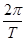 =2.……3分
=2.……3分将点
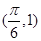 代入f(x)的解析式得sin
代入f(x)的解析式得sin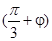 =1,
=1,∴
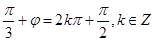 ,即
,即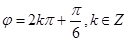 ,
,又|φ|<
 ,∴φ=
,∴φ= .………………………………5分
.………………………………5分故函数f(x)的解析式为f(x)=sin
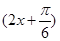 .…………………6分
.…………………6分(2)由f
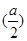 =
= ,得sin
,得sin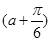 =
= ,由0<α<
,由0<α< ,得
,得 <α+
<α+ <
< ,
,∴cos
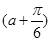 =
=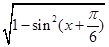 =
=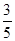 .………………………9分
.………………………9分∴cosα=[(α+
 )-
)- ]=cos
]=cos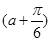 cos
cos +sin
+sin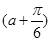 sin
sin =
=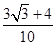 .………12分
.………12分
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
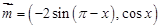 ,
,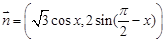 ,函数
,函数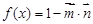 .
.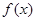 的解析式;
的解析式;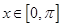 时,求
时,求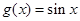 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.  ②
② ;
; ; ④
; ④ 其中“互为生成”函数的是( )
其中“互为生成”函数的是( ) 。
。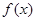 的最小正周期:
的最小正周期: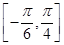 上的最大值和最小值。
上的最大值和最小值。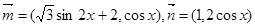 ,设函数
,设函数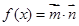 .
.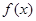 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;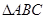 中,
中,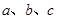 分别是角
分别是角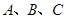 的对边,若
的对边,若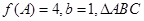 的面积
的面积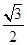 ,求a的值.
,求a的值. 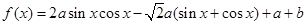 的定义域为
的定义域为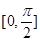 ,值域为
,值域为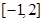 .
.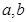 的值;
的值;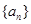 中,有
中,有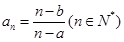 . 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
. 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.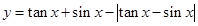 在区间
在区间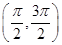 内的图象是 ( )
内的图象是 ( )
 ,且此函数的图象如右图,则点
,且此函数的图象如右图,则点 的坐标是( )
的坐标是( )




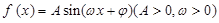 的图象如图所示,则
的图象如图所示,则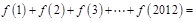 .
.