题目内容
等边三角形ABC的三个顶点在一个半径为1的球面上,O为球心,G为三角形ABC的中心,且 . 则
. 则 的外接圆的面积为
的外接圆的面积为
A. | B.2 | C. | D. |
C
解析试题分析:先确定△ABC的外接圆的半径,再求△ABC的外接圆的面积.解:设△ABC的外接圆的半径为r,则
∵O为球心,G为三角形ABC的中心,且OG= ,球的半径为1, R=
,球的半径为1, R=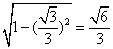 ∴△ABC的外接圆的面积为π×(
∴△ABC的外接圆的面积为π×(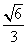 )×(
)×(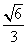 )=
)= ,故选C.
,故选C.
考点:球的截面圆
点评:本题考查球的截面圆,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
已知某几何体的三视图如图所示,则此几何体的体积是( )
A. | B. |
C.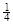 | D. |
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接球的表面积为 ( ) 
A. | B. | C. | D. |
点 在同一个球的球面,
在同一个球的球面, ,
,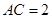 ,若四面体
,若四面体 体积的最大值为
体积的最大值为 ,则这个球的表面积为( )
,则这个球的表面积为( )
A. | B. | C. | D. |
如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,则该几何体的体积是
| A.24 | B.12 | C.8 | D.4 |





 三点,其中点
三点,其中点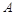 与
与 两点间的球面距离均为
两点间的球面距离均为 ,
, ,则球心到平面
,则球心到平面 的距离为( )
的距离为( )

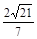





 的各顶点都在一个半径为
的各顶点都在一个半径为 的球面上,球心
的球面上,球心 在
在 上,
上, 底面
底面 ,
,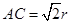 ,则球的体积与三棱锥体积之比是( )
,则球的体积与三棱锥体积之比是( )