题目内容
17．
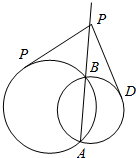如图，两圆相交于A、B两点，P为两圆公共弦AB上任一点，从P引两圆的切线PC、PD，若PC=2$\sqrt{2}$cm，则PD=2$\sqrt{2}$cm．
分析 先利用切割线定理得到PC2=PA•PB，PD2=PA•PB，进而得到PC=PD．
解答 解：由切割线定理可得，PC2=PA•PB，PD2=PA•PB，
∴PC2=PD2，即PC=PD=2$\sqrt{2}$（cm）．
故答案为：2$\sqrt{2}$．
点评 本题主要考查切割线定理的应用，是对基础知识的考查，需要有扎实的基本功．
练习册系列答案
相关题目
2．已知函数f（x）=|ex-e2x|，方程f2（x）+af（x）+a-1=0有四个不同的实数根，则a的取值范围为（ ）
| A． | （-∞，-$\frac{{e}^{2}+1}{e}$） | B． | （-∞，e2） | C． | （-2e2，1-e2） | D． | （1-e2，1） |
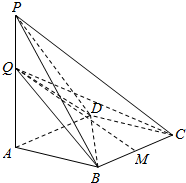已知四棱锥P-ABCD中，底面ABCD为∠ABC=$\frac{2}{3}$π的菱形，PA⊥平面ABCD，点Q在直线PA上．