题目内容
【题目】已知点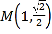 在椭圆上E:
在椭圆上E:![]() (
(![]() ),点
),点![]() 为平面上一点,O为坐标原点.
为平面上一点,O为坐标原点.
(1)当![]() 取最小值时,求椭圆E的方程;
取最小值时,求椭圆E的方程;
(2)对(1)中的椭圆E,P为其上一点,若过点![]() 的直线l与椭圆E相交于不同的两点S和T,且满足
的直线l与椭圆E相交于不同的两点S和T,且满足![]() (
(![]() ),求实数t的取值范围.
),求实数t的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据点点![]() 在椭圆上,则
在椭圆上,则![]() ,又
,又![]() 根据基本不等式求得当
根据基本不等式求得当![]() 时取得最小值,即可求得椭圆方程;
时取得最小值,即可求得椭圆方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,联立方程消元得
,联立方程消元得![]() ,利用根的判别式求出
,利用根的判别式求出![]() 的取值范围,再利用韦达定理求得
的取值范围,再利用韦达定理求得![]() ,
,![]() ,由
,由![]() 得
得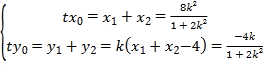 整理得到
整理得到![]() 的式子,代入椭圆方程,即可求出参数
的式子,代入椭圆方程,即可求出参数![]() 的取值范围.
的取值范围.
解:(1)点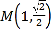 在椭圆上,则
在椭圆上,则![]()
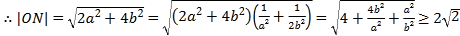
当且仅当![]() 时取等号
时取等号
由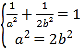 解得
解得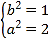
所以椭圆的方程为![]()
(2)由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,将直线方程代入椭圆方程得:
,将直线方程代入椭圆方程得:![]()
![]() 得
得![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
由![]() 得
得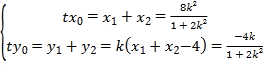
![]()
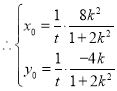 代入椭圆方程得
代入椭圆方程得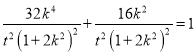
整理得![]()
由![]() 知
知![]()
![]()

【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
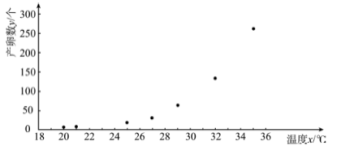
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.