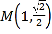题目内容
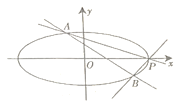
【题目】设有一组圆![]() ,下列四个命题:①存在一条定直线与所有的圆均相切;②存在一条定直线与所有的圆均相交;③存在一条定直线与所有的圆均不相交;④所有的圆均不经过原点;其中真命题的个数为( )
,下列四个命题:①存在一条定直线与所有的圆均相切;②存在一条定直线与所有的圆均相交;③存在一条定直线与所有的圆均不相交;④所有的圆均不经过原点;其中真命题的个数为( )
A.1B.2C.3D.4
【答案】B
【解析】
根据圆的方程找出圆心坐标,发现满足条件的所有圆的圆心在一条直线上,所以这条直线与所有的圆都相交,②正确;根据图象可知这些圆互相内含,不存在一条定直线与所有的圆均相切,不存在一条定直线与所有的圆均不相交,所以①③错;利用反证法,假设经过原点,将![]() 代入圆的方程,因为左边为奇数,右边为偶数,故不存在
代入圆的方程,因为左边为奇数,右边为偶数,故不存在![]() 使上式成立,假设错误,则圆不经过原点,④正确.
使上式成立,假设错误,则圆不经过原点,④正确.
解:根据题意得:圆心![]() ,圆心在直线
,圆心在直线![]() 上,故存在直线
上,故存在直线![]() 与所有圆都相交,选项②正确;
与所有圆都相交,选项②正确;
考虑两圆的位置关系,
圆![]() :圆心
:圆心![]() ,半径为
,半径为![]() ,
,
圆![]() :圆心
:圆心![]() ,
,![]() ,即
,即![]() ,半径为
,半径为![]() ,
,
两圆的圆心距![]() ,
,
两圆的半径之差![]() ,
,
任取![]() 或2时,
或2时,![]() ,
,![]() 含于
含于![]() 之中,选项①错误;
之中,选项①错误;
若![]() 取无穷大,则可以认为所有直线都与圆相交,选项③错误;
取无穷大,则可以认为所有直线都与圆相交,选项③错误;
将![]() 带入圆的方程,则有
带入圆的方程,则有![]() ,即
,即![]() ,
,
因为左边为奇数,右边为偶数,故不存在![]() 使上式成立,即所有圆不过原点,选项④正确.
使上式成立,即所有圆不过原点,选项④正确.
则正确命题是②④.
故选:![]() .
.

【题目】为进一步优化教育质量平台,更好的服务全体师生,七天网络从甲、乙两所学校各随机抽取100名考生的某次“四省八校”数学考试成绩进行分析,分别绘制的频率分布直方图如图所示.
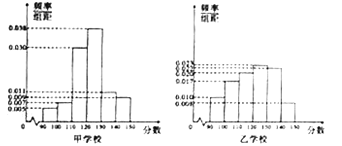
为了更好的测评各个学校数学学科的教学质量,该公司依据每一位考生的数学测试分数将其划分为“![]() ,
,![]() ,
,![]() ”三个不同的等级,并按照不同的等级,设置相应的对学校数学学科教学质量贡献的积分,如下表所示.
”三个不同的等级,并按照不同的等级,设置相应的对学校数学学科教学质量贡献的积分,如下表所示.
测试分数 | 分数对应的等级 | 贡献的积分 |
|
| 1分 |
|
| 2分 |
|
| 3分 |
(1)用样本的频率分布估计总体的频率分布,若将甲学校考生的数学测试等级划分为“![]() 等”和“非
等”和“非![]() 等”两种,利用分层抽样抽取10名考生,再从这10人随机抽取3人,求3人中至少1人数学测试为“
等”两种,利用分层抽样抽取10名考生,再从这10人随机抽取3人,求3人中至少1人数学测试为“![]() 等”的概率;
等”的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,若从乙学校全体考生中随机抽取3人,记3人中数学测试等级为“![]() 等”的人数为
等”的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)根据考生的数学测试分数对学校数学学科教学质量贡献的积分规则,分别记甲乙两所学校数学学科质量的人均积分为![]() 和
和![]() ,用样本估计总体,求
,用样本估计总体,求![]() 和
和![]() 的估计值,并以此分析,你认为哪所学校本次数学教学质量更加出色?
的估计值,并以此分析,你认为哪所学校本次数学教学质量更加出色?