题目内容
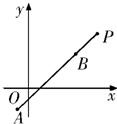
已知点A(-2,3),B(3,2),过点P(0,-2)的直线l与线段AB有公共点,求直线l的斜率的取值范围及倾斜角的取值范围.
解析:
|
思路 由题中条件“直线l与线段AB有公共点”展开联想:①因为直线l过定点P(0,-2)与线段AB的公共点在AB上,可用运动变化的观点,求出符合条件的所有直线的斜率;②从整体上考虑,由题中交点M在线段AB上的数学模型,联想到M为
解法一 如上图所示,直线PA的斜率kPA= 所以直线l的斜率的取值范围是(-∞,- 解法二 如上图,设直线l与线段AB交于点M,则M是 由定比分点坐标公式得M( 又直线l过点P(0,-2),故l的斜率k= 当点M不与B点重合时,λ≥0,即 当点M与B重合时,λ不存在,可直接求出kBP= 以上同解法一. 评析 (1)求直线倾斜角时,一要注意倾斜角的取值范围,二要注意与之相关的三角函数及反三角函数的有关概念. (2)对于过两定点的直线的倾斜角问题,一般应先考虑斜率是否存在.这是隐含在题中的一个分类因素,很容易被忽视,应引起重视. (3)数形结合是解析几何中的重要思想,解题时,可根据问题的需要,借助图形及图形性质直观作出判断,明确解题思想,既能避免繁杂冗长的计算与推理,又能考证结论是否完善. |

 名校课堂系列答案
名校课堂系列答案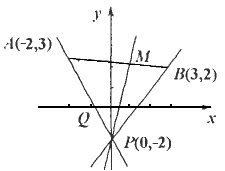
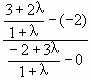 =
=