题目内容
已知点A（2，3），B（-3，-2），若直线l过点P（1，1），且与线段AB相交，求直线l的斜率k的取值范围．分析：本题考查的知识点是数形结合思想，及直线斜率的变化，我们可以在平面直角坐标系中画出图象，根据图象分析A，B，C三点之间的关系，不难给出直线l的斜率k的取值范围．
解答：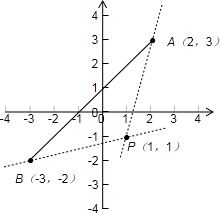
解：在平面直角坐标系中画出图象如下图：
设，直线PA的斜率为k1，直线PB的斜率为k2，则
k1=2，k2=
直线l的斜率k的取值范围为：（-∞，
]∪[2，+∞）
故答案为：（-∞，
]∪[2，+∞）
解：在平面直角坐标系中画出图象如下图：设，直线PA的斜率为k1，直线PB的斜率为k2，则
k1=2，k2=
| 3 |
| 4 |
直线l的斜率k的取值范围为：（-∞，
| 3 |
| 4 |
故答案为：（-∞，
| 3 |
| 4 |
点评：已知点A，B，直线l过点P（m，n），且与线段AB相交，求直线l的斜率k的取值范围分两种情况：①若A，B在直线x=m的同侧时，如图所示：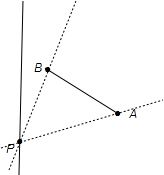
或
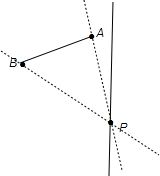
设直线PA的斜率为k1，直线PB的斜率为k2，则[k1，k2]②若A，B在直线x=m的异侧时，（如本题）直线l的斜率k的取值范围为：（-∞，k2]∪[k1，+∞）
或设直线PA的斜率为k1，直线PB的斜率为k2，则[k1，k2]②若A，B在直线x=m的异侧时，（如本题）直线l的斜率k的取值范围为：（-∞，k2]∪[k1，+∞）
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
