题目内容
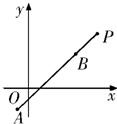
已知点A(-2,-3),B(3,2),直线l过点P(-1,5)且与线段AB有交点,设直线l的斜率为k,则k的取值范围是
k≤-
或k≥8
| 3 |
| 4 |
k≤-
或k≥8
.| 3 |
| 4 |
分析:先根据A,B,P的坐标分别求得直线AP和BP的斜率,设l与线段AB交于M点,M由A出发向B移动,斜率越来越小,其间会出现PM平行y轴,此时无斜率.求得k的一个范围,过了这点,斜率由负无穷大向-
进发求得k的另一个范围,最后综合可得答案.
| 3 |
| 4 |
解答: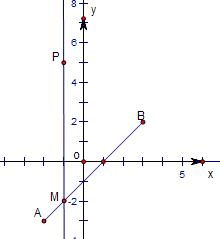 解:直线AP的斜率k=
解:直线AP的斜率k=
=8,
直线BP的斜率k=
=-
设l与线段AB交于M点,M由A出发向B移动,斜率越来越小,
其间会出现PM平行y轴,此时无斜率,即k≥8,
过了这点,斜率由负无穷大向-
进发,即k≤-
.
综上,k≤-
或k≥8.
故答案为:k≤-
或k≥8.
 解:直线AP的斜率k=
解:直线AP的斜率k=| 5+3 |
| -1+2 |
直线BP的斜率k=
| 5-2 |
| -1-3 |
| 3 |
| 4 |
设l与线段AB交于M点,M由A出发向B移动,斜率越来越小,
其间会出现PM平行y轴,此时无斜率,即k≥8,
过了这点,斜率由负无穷大向-
| 3 |
| 4 |
| 3 |
| 4 |
综上,k≤-
| 3 |
| 4 |
故答案为:k≤-
| 3 |
| 4 |
点评:本题主要考查了直线的斜率,解题的关键是利用了数形结合的思想,解题过程较为直观.

练习册系列答案
相关题目