设函数m(x)=$\left\{\begin{array}{l}{{x}^{2}.{x}^{2}≤{2}^{x}}\\{{2}^{x}.{2}^{x}＜{x}^{2}}\end{array}\right.$.则mA．0B．$\frac{1}{2}$C．1D．2 题目和参考答案——青夏教育精英家教网—

题目内容

2．设函数m（x）=$\left\{\begin{array}{l}{{x}^{2}，{x}^{2}≤{2}^{x}}\\{{2}^{x}，{2}^{x}＜{x}^{2}}\end{array}\right.$，则m（x）的最小值为（　　）

A．

B．

$\frac{1}{2}$

C．

D．

分析由题意可得m（x）为函数y=x²和y=2^x的较小者，作图可得．

解答解：由题意可得m（x）=$\left\{\begin{array}{l}{{x}^{2}，{x}^{2}≤{2}^{x}}\\{{2}^{x}，{2}^{x}＜{x}^{2}}\end{array}\right.$为函数y=x²和y=2^x的较小者，
作图（图中红色线）可知，m（x）的最小值为0，
故选：A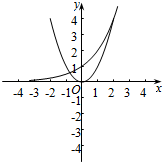

点评本题考查函数的最值求解，作图是解决问题的关键，属基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

13．已知在△ABC中，sinA+cosA=$\frac{{\sqrt{5}}}{5}$
（Ⅰ）求sinA-cosA的值；
（Ⅱ）求$\frac{{5{{sin}^2}A+sin（A-\frac{π}{2}）cos（A+\frac{3π}{2}）-5{{cos}^2}A}}{sinAcosA}$的值．

10．设函数f（x）=ln（1+x）-ln（1-x）．
（1）求函数的定义域；
（2）判断函数的奇偶性，并说明理由．

17．过点（2，-1）引直线与抛物线x²=4y只有一个公共点，这样的直线共有3条．

7．已知cos（π+x）=$\frac{4}{5}$，x∈（π，2π），则cos（$\frac{π}{2}-x$）=（　　）

14．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|，＜$\overrightarrow{c}-\overrightarrow{a}，\overrightarrow{c}-\overrightarrow{b}$＞=$\frac{2π}{3}$，则$\frac{|\overrightarrow{c}|}{|\overrightarrow{a}|}$的最大值为$\frac{2\sqrt{3}}{3}$．

11．下列有关命题的说法正确的是（　　）

	A．	命题“若x²=1，则x=1”的否命题为：“若x²=1，则x≠1”
	B．	命题“?x∈R，使得x²+x+1＜0”的否定是：“?x∈R 均有x²+x+1＜0”
	C．	在△ABC中，“A＞B”是“sinA＞sinB”的充要条件
	D．	“x≠2或y≠1”是“x+y≠3”既不充分也不必要条件

12．为了解某校学生喜爱打篮球是否与性别有关，采用随机抽样方法抽取了50名学生进行问卷调查，得到如下的列联表：

	喜爱打篮球	不喜爱打篮球	合计
男生		5
女生	10
合计			50

已知在这50名学生中随机抽取1人，抽到喜爱打篮球的学生的概率为$\frac{3}{5}$．
（Ⅰ）请将上面的列联表补充完整；
（Ⅱ）是否有99.5%的把握认为喜爱打篮球与性别有关？说明你的理由；
（Ⅲ）记不喜爱打篮球的5名男生分别为A、B、C、D、E，这5名男生喜爱打乒乓球，
如果从他们当中任选2人作为一对组合参加乒乓球男子双打比赛，求A、B中恰好有1人被选中的概率．
下面的临界值表供参考：

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式：K²=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

试题分类