题目内容
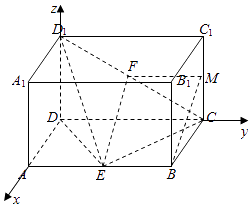
【题目】在长方体ABCD﹣A1B1C1D1中，E，F分别是AB，CD1的中点，AA1=AD=1，AB=2． 
（1）求证：EF∥平面BCC1B1；
（2）求证：平面CD1E⊥平面D1DE；
（3）在线段CD1上是否存在一点Q，使得二面角Q﹣DE﹣D1为45°，若存在，求 
的值，不存在，说明理由．
【答案】
（1）证明：过F作FM∥C1D1交CC1于M，连结BM，
∵F是CD1的中点，∴FM∥C1D1，FM= 
C1D1，
又∵E是AB中点，∴BE∥C1D1，BE= C1D1，
∴BE∥FM，BE=FM，EBMF是平行四边形，
∴EF∥BM
又BM在平面BCC1B1内，∴EF∥平面BCC1B1．
（2）证明：∵D1D⊥平面ABCD，CE在平面ABCD内，
∴D1D⊥CE
在矩形ABCD中，DE2=CE2=2，
∴DE2+CE2=4=CD2，
∴△CED是直角三角形，∴CE⊥DE，
∴CE⊥平面D1DE，
∵CE在平面CD1E内，∴平面CD1E⊥平面D1DE．
（3）解：以D为原点，DA、DC、DD1所在直线为x轴、y轴、z轴建立坐标系，
则C（0，2，0），E（1，1，0），D1（0，0，1）
平面D1DE的法向量为 
=（﹣1，1，0），
设 
=（0，2λ，﹣λ），（0＜λ＜1），则Q（0，2λ，1﹣λ），
设平面DEQ的法向量为 
=（x，y，z），
则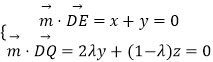 
，令y=1，则 =（﹣1，1， 
），
∵二面角Q﹣DE﹣D1为45°，∴cos45°= 
= 
= 
，
由于0＜λ＜1，∴ 
﹣1，
∴线段CD1上存在一点Q，使得二面角Q﹣DE﹣D1为45°，且 
= 
．
【解析】（1）过F作FM∥C1D1交CC1于M，连结BM，推导出EBMF是平行四边形，从而EF∥BM，由此能证明EF∥平面BCC1B1 ． （2）推导出D1D⊥CE，CE⊥DE，从而CE⊥平面D1DE，由此能证明平面CD1E⊥平面D1DE．（3）以D为原点，DA、DC、DD1所在直线为x轴、y轴、z轴建立坐标系，利用向量法能求出线段CD1上存在一点Q，使得二面角Q﹣DE﹣D1为45°，且 = ．
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本，需要知道平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直．
