题目内容
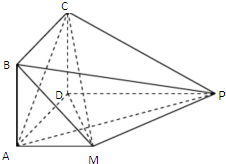 如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=| 1 |
| 2 |
(1)求证:平面ABCD⊥平面AMPD;
(2)求点A到面CMP的距离.
考点:点、线、面间的距离计算,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)只要证明CD⊥平面AMPD即可;
(2)要求点A到面CMP的距离,只要求三棱锥A-CMP的高,通过计算可得.
(2)要求点A到面CMP的距离,只要求三棱锥A-CMP的高,通过计算可得.
解答:
(1)证明:∵PM⊥平面CDM,且CD?平面CDM,∴PM⊥CD,又ABCD是正方形,∴CD⊥AD,∴CD⊥平面AMPD,又CD?平面ABCD,∴平面ABCD⊥平面AMPD;
解:(2)设三棱锥A-CMP的高为h,
由(1)知CD⊥平面AMPD,PM⊥平面CDM∴PM⊥CM,PM⊥DM,
又MA=AD=
PD=2.所以DM=2
,CM=2
,PM=2
,故S△AMP=
AM×AD=2,S △CMP=2
,∴h=
=
=
,
故三棱锥A-CMP的高为
,点A到面CMP的距离为
.
解:(2)设三棱锥A-CMP的高为h,
由(1)知CD⊥平面AMPD,PM⊥平面CDM∴PM⊥CM,PM⊥DM,
又MA=AD=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 6 |
| S△AMP×CD |
| S△CMP |
| 2×2 | ||
2
|
| ||
| 3 |
故三棱锥A-CMP的高为
| ||
| 3 |
| ||
| 3 |
点评:本题考查了面面垂直的判定和通过三棱锥的体积求点到面的距离,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
正方体ABCD-A1B1C1D1中,直线BC1与平面A1BD所成角的余弦值为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设向量
,
满足|
+
|=
,|
-
|=
,则
•
=( )
| a |
| b |
| a |
| b |
| 15 |
| a |
| b |
| 11 |
| a |
| b |
| A、1 | B、2 | C、3 | D、5 |
已知数列{an}的通项公式为an=
(n∈N+),若前n项和为10,则项数n为( )
| 1 | ||||
|
| A、100 | B、110 |
| C、120 | D、130 |